题目内容
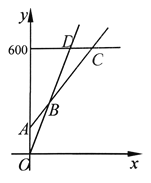
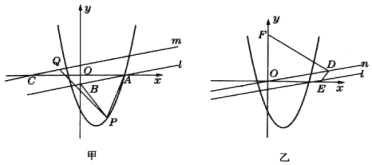
【题目】如图所示,在平面直角坐标系中,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于
轴交于![]() 点,经过点
点,经过点![]() 的抛物线
的抛物线![]() 上有一动点
上有一动点![]() ,且点
,且点![]() 在直线
在直线![]() 的下方.
的下方.
(1)平移直线![]() 经过点
经过点![]() ,得到直线
,得到直线![]() ,点
,点![]() 为直线
为直线![]() 上一个动点,连接
上一个动点,连接![]() ,当
,当![]() 面积最大时,求
面积最大时,求![]() 的最小值.
的最小值.
(2)平移直线![]() 经过原点,得到直线
经过原点,得到直线![]() ,点
,点![]() 是直线
是直线![]() 上一点,且
上一点,且![]() 点横坐标为6,点
点横坐标为6,点![]() 在
在![]() 轴上,点
轴上,点![]() 在
在![]() 轴上,当
轴上,当![]() 时,抛物线上是否存在点
时,抛物线上是否存在点![]() ,使四边形
,使四边形![]() 是矩形?如果存在,请求出点
是矩形?如果存在,请求出点![]() 的坐标,如果不存在,请说明理由.
的坐标,如果不存在,请说明理由.
【答案】(1)![]() 的最小值为
的最小值为![]() ;(2)点
;(2)点![]() 的坐标为
的坐标为![]() 或
或![]() .
.
【解析】
(1)设![]() ,根据
,根据![]() 列出函数关系式求出当
列出函数关系式求出当![]() 的面积有最大值时,
的面积有最大值时,![]() ,求出直线
,求出直线![]() 的解析式,过点
的解析式,过点![]() 作
作![]() 轴,易得
轴,易得![]() ,然后根据相似三角形的性质得
,然后根据相似三角形的性质得![]() ,进而可求出结论;
,进而可求出结论;
(2)过![]() 作
作![]() 轴,
轴,![]() 轴,易得
轴,易得![]() 且相似比为1:3.然后分点
且相似比为1:3.然后分点![]() 在点
在点![]() 的左侧时和点
的左侧时和点![]() 在点
在点![]() 的右侧时两种情况求解即可.
的右侧时两种情况求解即可.
(1)设![]() ,
,
![]()
![]()
![]()
![]() ,
,
![]() 当
当![]() 时,
时,![]() 的面积有最大值.
的面积有最大值.
![]() ,
,
![]() 平移直线
平移直线![]() 得到直线
得到直线![]() ,且过点
,且过点![]() ,
,
易得直线![]() .
.
过点![]() 作
作![]() 轴,
轴,
易得![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
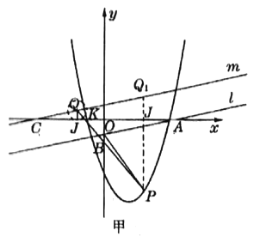
由图知,![]() ,
,![]() ,
,
![]() 当
当![]() 轴时,
轴时,![]() ,
,![]() 重合,
重合,
此时![]() 有最小值等
有最小值等![]() .
.
![]() 的最小值为
的最小值为![]() .
.
(2)过![]() 作
作![]() 轴,
轴,![]() 轴,
轴,
![]() 直线
直线![]() 平移后过原点得到直线
平移后过原点得到直线![]() ,
,
![]() 直线
直线![]() ,代入
,代入![]() .
.
![]() 点坐标为
点坐标为![]() ,
,![]() ,
,![]() .
.
![]() ,
,
![]() 易得
易得![]() 且相似比为1:3.
且相似比为1:3.
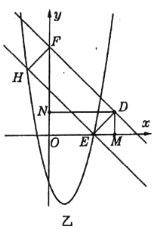
如图乙所示,
点![]() 在点
在点![]() 的左侧时,设
的左侧时,设![]() ,则
,则![]() .
.
![]() ,
,
![]() .
.
![]() .
.
![]() 四边形
四边形![]() 为矩形,
为矩形,
![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,![]() .
.
将点![]() 的坐标代入抛物线的解析式得,
的坐标代入抛物线的解析式得,
![]() ,
,
解得:![]() ,
,![]() (舍去).
(舍去).
![]() ,
,
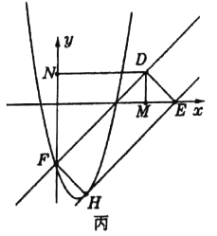
如图丙所示:点![]() 在点
在点![]() 的右侧时,设
的右侧时,设![]() ,
,
则![]() .
.
![]() ,
,
![]() .
.
![]() .
.
![]() 四边形
四边形![]() 为矩形,
为矩形,
![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,![]() .
.
将点![]() 的坐标代人抛物线的解析式得,
的坐标代人抛物线的解析式得,
![]()
![]() ,
,
解得:![]() (舍去)或
(舍去)或![]() .
.
![]() .
.
综上所述,
点![]() 的坐标为
的坐标为![]() 或
或![]() .
.

【题目】合肥市教育教学研究室为了了解该市所有毕业班学生参加2019年安徽省中考一模考试的数学成绩情况(满分:150分,等次:![]() 等,130分
等,130分![]() 150分;
150分;![]() 等,110分
等,110分![]() 129分;C等,90分
129分;C等,90分![]() 109分;D等,89分及以下),从该市所有参考学生中随机抽取部分学生进行调查,并根据调查结果制作了如下的统计图表(部分信息未给出):
109分;D等,89分及以下),从该市所有参考学生中随机抽取部分学生进行调查,并根据调查结果制作了如下的统计图表(部分信息未给出):
2019年合肥市一模数学成绩频数分布表
等次 | 频数 | 频率 |
| 0.2 | |
| ||
| 6 | |
| 2 | 0.1 |
合计 | 1 |
2019年合肥市一模教学成绩频数分布直方图
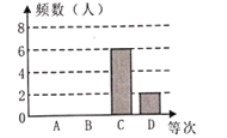
根据图表中的信息,下列说法不正确的是( )
A. 这次抽查了20名学生参加一模考试的数学成绩
B. 这次一模考试中,考试数学成绩为![]() 等次的频率为0.4
等次的频率为0.4
C. 根据频数分布直方图制作的扇形统计图中等次![]() 所占的圆心角为
所占的圆心角为![]()
D. 若全市有20000名学生参加中考一模考试,则估计数学成绩达到![]() 等次及以上的人数有12000人
等次及以上的人数有12000人