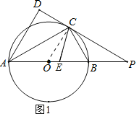
题目内容
【题目】如图,![]() 是
是![]() 的直径,点
的直径,点![]() 是
是![]() 上一点,
上一点,![]() 与过点
与过点![]() 的切线垂直,垂足为点
的切线垂直,垂足为点![]() ,直线
,直线![]() 与
与![]() 的延长线相交于点
的延长线相交于点![]() ,
,![]() 平分
平分![]() ,交
,交![]() 于点
于点![]() .
.
![]() 求证:
求证:![]() 平分
平分![]() ;
;
![]() 求证:
求证:![]() 是等腰三角形.
是等腰三角形.

【答案】见解析
【解析】
(1)依据切线的性质可知OC⊥DC,然后可证明AD∥OC,依据平行线的性质可得到∠DAC=∠ACO,然后依据OA=OC可证明∠OAC=∠ACO,通过等量代换可证明AC平分∠DAB;
(2)依据直径所对的圆周角等于90°可证明∠ACB=90°,然后依据同角的余角相等可证明∠DAC=∠BCP,由(1)可知AC平分∠DAB,从而得到∠CAE=∠BCP,然后结合∠ACE=∠ECB可证明∠PCE=∠PEC.
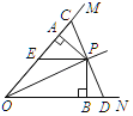
![]() 如图
如图![]() 所示:连接
所示:连接![]() .
.
∵![]() 切
切![]() 于点
于点![]() ,
,
∴![]() .
.
又∵![]() ,
,
∴![]() .
.
∴![]() .
.
又∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
即![]() 平分
平分![]() .
.
![]() ∵
∵![]() ,
,
∴![]() .
.
又∵![]() 为
为![]() 的直径,
的直径,
∴![]() .
.
∴![]() ,
,
∴![]() .
.
又∵![]() ,
,
∴![]() .
.
∵![]() 平分
平分![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
即![]() 是等腰三角形.
是等腰三角形.

练习册系列答案
 初中暑期衔接系列答案
初中暑期衔接系列答案
相关题目