题目内容
已知⊙O半径为1,AB是⊙O的一条弦,且AB=
,则弦AB所对的圆周角度数是 .
| 2 |
考点:圆周角定理,等腰直角三角形
专题:分类讨论
分析:根据题意画出图形,由OC垂直于AB,利用垂径定理得到C为AB的中点,求出AC的长,在直角三角形AOC中,利用勾股定理求出OC=AC,确定出三角形AOC为等腰直角三角形,同理三角形BOC为等腰直角三角形,确定出∠AOB度数,利用圆周角定理即可求出∠ADB与∠AEB的度数.
解答: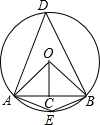 解:如图所示,
解:如图所示,
∵OC⊥AB,
∴C为AB的中点,即AC=BC=
AB=
,
在Rt△AOC中,OA=1,AC=
,
根据勾股定理得:OC=
=
=
,即OC=AC,
∴△AOC为等腰直角三角形,
∴∠AOC=45°,
同理∠BOC=45°,
∴∠AOB=∠AOC+∠BOC=90°,
∵∠AOB与∠ADB都对
,
∴∠ADB=
∠AOB=45°,
∵大角∠AOB=270°,
∴∠AEB=135°,
∴弦AB所对的圆周角为45°或135°.
故答案为:45°或135°.
 解:如图所示,
解:如图所示,∵OC⊥AB,
∴C为AB的中点,即AC=BC=
| 1 |
| 2 |
| ||
| 2 |
在Rt△AOC中,OA=1,AC=
| ||
| 2 |
根据勾股定理得:OC=
| OA2-AC2 |
12-(
|
| ||
| 2 |
∴△AOC为等腰直角三角形,
∴∠AOC=45°,
同理∠BOC=45°,
∴∠AOB=∠AOC+∠BOC=90°,
∵∠AOB与∠ADB都对
 |
| AB |
∴∠ADB=
| 1 |
| 2 |
∵大角∠AOB=270°,
∴∠AEB=135°,
∴弦AB所对的圆周角为45°或135°.
故答案为:45°或135°.
点评:本题考查的是圆周角定理,在解答此题时要进行分类讨论,不要漏解.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
一条弧所对的圆心角为60°,那么这条弧所对的圆周角为( )
| A、30° | B、60° |
| C、120° | D、150° |
计算(ab)(3a2b2)3的结果是( )
| A、-3a3b3 |
| B、27a7b7 |
| C、-27a7b7 |
| D、-3a7b7 |
下列说法:①-4的相反数;②-1与-4的乘积;③-4的绝对值;④(-2)2.其中结果与-(-4)相同的有( )
| A、1个 | B、2个 | C、3个 | D、4个 |
 如图是每个面上都有一个汉字的正方体的一种平面展开图,那么在原正方体中和“国”字相对的面是
如图是每个面上都有一个汉字的正方体的一种平面展开图,那么在原正方体中和“国”字相对的面是 已知在△ABC中,AB=10,AC=9,BC=7,在△ADE中,AD=4,AE=
已知在△ABC中,AB=10,AC=9,BC=7,在△ADE中,AD=4,AE=