题目内容
（1）计算：
（2）解分式方程：
．
解：（1）原式=
，
=
，
=1；
（2）设
，则原方程变形为y2-2y-8=0，
解这个方程得，y1=4，y2=-2．
当y=4时，
，解得
；
当y=-2时，
，解得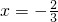
．
经检验
，
都是原方程的根．
分析：（1）利用二次根式的性质进行化简，以及负指数幂的性质和绝对值得性质进行运算即可；
（2）利用换元法设，则原方程变形为y2-2y-8=0，求出y的值，进而得出x的值即可．
点评：此题主要考查了换元法解分式方程以及负指数、绝对值的化简、二次根式的化简等知识，根据已知熟练利用换元法求出是解题关键．
，=
，=1；
（2）设
，则原方程变形为y2-2y-8=0，解这个方程得，y1=4，y2=-2．
当y=4时，
，解得；当y=-2时，
，解得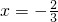．经检验
，都是原方程的根．分析：（1）利用二次根式的性质进行化简，以及负指数幂的性质和绝对值得性质进行运算即可；
（2）利用换元法设
，则原方程变形为y2-2y-8=0，求出y的值，进而得出x的值即可．点评：此题主要考查了换元法解分式方程以及负指数、绝对值的化简、二次根式的化简等知识，根据已知熟练利用换元法求出是解题关键．
练习册系列答案
相关题目
