题目内容
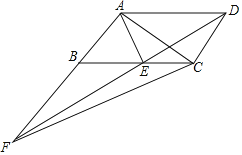
【题目】如图E是平行四边形
边BC上一点，且
，连接AE，并延长AE与DC的延长线交于点F， 
．
（1）请判断
的形状，并说明理由；
（2）求
的各内角的大小．
【答案】（1）
为等边三角形，见解析；（2）60°，120°，60°，120°
【解析】
(1)先求出∠BAE=60°，然后利用等边对等角，由AB=BE，再求出∠AEB=∠FEC=60°即可；
(2)求出∠BCD=120°后，再利用平行四边形的邻角互补，对角相等即可求出其余各角.
解：(1)为等边三角形，理由如下：
∵四边形
是平行四边形
∴ 
∴
∵
又
∴
，
∴
∴△ECF为等边三角形.
(2)由第(1)问知，
∴
∵四边形ABCD是平行四边形
∴
，AB∥CD
∴
∴
各内角的大小分别是60°，120°，60°，120°.
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
