题目内容
?ABCD中,AB=10(AB>AD),AD与BC之间的距离为6,点E在线段AB上移动,以E为圆心,AE长为半径作⊙E.(1)如图1,若⊙E与BC所在的直线相切,求AE之长;
(2)如图2,若E点是∠DCB的角平分线与AB的交点,这时若⊙E与BC所在的直线相切于点F.
①试说明此时⊙E也与CD所在的直线相切;
②求此时AD的长.

【答案】分析:(1)如图1,过点B作BG⊥AD于点G,连接EF.利用平行线AD∥CB的性质推知内错角∠DAB=∠ABF;然后在Rt△ABG和Rt△BEF中根据三角函数的定义求得 =
= =
= ,利用比例的性质即可求得AE的值;
,利用比例的性质即可求得AE的值;
(2)①如图2,过圆心E作EG垂直于CD所在的直线于点G,连接EF.利用切线的性质、角平分线的性质推知GE=EF,即点G也在⊙E上,所以⊙E与CD所在的直线相切;
②根据图形知BE=AB-AE= ;由平行线的性质、平行四边形的性质以及角平分线的性质推知AD=BC=EB=
;由平行线的性质、平行四边形的性质以及角平分线的性质推知AD=BC=EB= .
.
解答: 解:(1)如图1,过点B作BG⊥AD于点G,连接EF.
解:(1)如图1,过点B作BG⊥AD于点G,连接EF.
∵AD与BC之间的距离为6,
∴BG=6;
∴sin∠DAB= =
= =
= ;
;
又∵CF是⊙E的切线,
∴EF⊥CF,
∴sin∠BEF= ;
;
∵四边形ABCD是平行四边形,
∴AD∥BC(平行四边形的对边相互平行),
∴∠DAB=∠ABF(两直线平行,内错角相等);
∵AE=EF(⊙E的半径),
∴ =
= ,即
,即 =
= ,
,
∴AE= ;
;
(2)①如图2,过圆心E作EG垂直于CD所在的直线于点G,连接EF.
∵CF是⊙E的切线,点F是切点,
∴EF⊥CF;
又∵E点是∠DCB的角平分线与AB的交点,
∴EG=EF(角平分线上的点到该角两边的距离相等),
∴点G在⊙E上,
∴⊙E与CD所在的直线相切;
②如图2,延长FE交AD于点H.
∵EF⊥CF,CF∥AD,
∴HF⊥AD;
又∵ =
= (平行线截线段成比例),HE=6,AE=EF(⊙E的半径),
(平行线截线段成比例),HE=6,AE=EF(⊙E的半径),
∴ =
= ,
,
∴AE= ,
,
∴BE=AB-AE=10- =
= ;
;
∵CD∥AB(平行四边形的对边平行),
∴∠DCE=∠CEB;
∵∠DCE=∠BCE(角平分线的性质),
∴∠CEB=∠ECB(等量代换),
∴EB=CB(等角对等边);
∵AD=BC(平行四边形的对边相等),
∴AD=BE= .
.
点评:本题考查了圆的综合题:解直角三角形、切线的判定与性质、全等三角形的判定与性质以及角平分线的综合运用.
 =
= =
= ,利用比例的性质即可求得AE的值;
,利用比例的性质即可求得AE的值;(2)①如图2,过圆心E作EG垂直于CD所在的直线于点G,连接EF.利用切线的性质、角平分线的性质推知GE=EF,即点G也在⊙E上,所以⊙E与CD所在的直线相切;
②根据图形知BE=AB-AE=
 ;由平行线的性质、平行四边形的性质以及角平分线的性质推知AD=BC=EB=
;由平行线的性质、平行四边形的性质以及角平分线的性质推知AD=BC=EB= .
.解答:
 解:(1)如图1,过点B作BG⊥AD于点G,连接EF.
解:(1)如图1,过点B作BG⊥AD于点G,连接EF.∵AD与BC之间的距离为6,
∴BG=6;
∴sin∠DAB=
 =
= =
= ;
;又∵CF是⊙E的切线,
∴EF⊥CF,
∴sin∠BEF=
 ;
;∵四边形ABCD是平行四边形,
∴AD∥BC(平行四边形的对边相互平行),
∴∠DAB=∠ABF(两直线平行,内错角相等);
∵AE=EF(⊙E的半径),
∴
 =
= ,即
,即 =
= ,
,∴AE=
 ;
;(2)①如图2,过圆心E作EG垂直于CD所在的直线于点G,连接EF.
∵CF是⊙E的切线,点F是切点,
∴EF⊥CF;
又∵E点是∠DCB的角平分线与AB的交点,
∴EG=EF(角平分线上的点到该角两边的距离相等),
∴点G在⊙E上,
∴⊙E与CD所在的直线相切;
②如图2,延长FE交AD于点H.
∵EF⊥CF,CF∥AD,
∴HF⊥AD;
又∵
 =
= (平行线截线段成比例),HE=6,AE=EF(⊙E的半径),
(平行线截线段成比例),HE=6,AE=EF(⊙E的半径),∴
 =
= ,
,∴AE=
 ,
,∴BE=AB-AE=10-
 =
= ;
;∵CD∥AB(平行四边形的对边平行),
∴∠DCE=∠CEB;
∵∠DCE=∠BCE(角平分线的性质),
∴∠CEB=∠ECB(等量代换),
∴EB=CB(等角对等边);
∵AD=BC(平行四边形的对边相等),
∴AD=BE=
 .
.点评:本题考查了圆的综合题:解直角三角形、切线的判定与性质、全等三角形的判定与性质以及角平分线的综合运用.

练习册系列答案
 导学与测试系列答案
导学与测试系列答案 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案
相关题目
如图,在?ABCD中,AB:AD=3:2,∠ADB=60°,那么cosA的值等于( )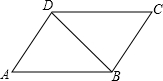

A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
 7、如图,平行四边形ABCD中,AB=3,BC=5,AC的垂直平分线交AD于E,若AC=4则.①△CDE的周长比△CDA的周长小4,②∠ACD=90°;③AE=ED=CE;④四边形ABCD面积是12.则上述结论正确的是( )
7、如图,平行四边形ABCD中,AB=3,BC=5,AC的垂直平分线交AD于E,若AC=4则.①△CDE的周长比△CDA的周长小4,②∠ACD=90°;③AE=ED=CE;④四边形ABCD面积是12.则上述结论正确的是( ) 14、如图,在矩形ABCD中,AB=6cm,将矩形ABCD折叠,使点B与点D重合,点C落在C′处,若AE:BE=1:2,则折痕EF的长为
14、如图,在矩形ABCD中,AB=6cm,将矩形ABCD折叠,使点B与点D重合,点C落在C′处,若AE:BE=1:2,则折痕EF的长为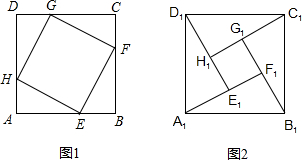
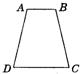 5、如图,在等腰梯形ABCD中,AB∥DC,AB=998,DC=1001,AD=1999,点P在线段AD上,则满足条件∠BPC=90°的点P的个数为( )
5、如图,在等腰梯形ABCD中,AB∥DC,AB=998,DC=1001,AD=1999,点P在线段AD上,则满足条件∠BPC=90°的点P的个数为( )