Question

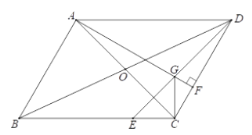
【题目】在平行四边形中，对角线、交于点、是上一点，连接，点在边上，且交于点，连接，已知，.

（1）若，，求的长；

（2）求证：.

Answer 1

【答案】（1）；（2）见解析

【解析】

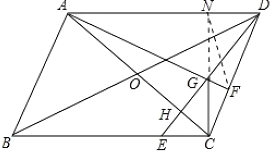
（1）延长CG交AD于N，连接NF，AC交DE于H，证出∠DGN＝∠CGE＝45°，GC⊥AD，得出∠GFD＝90°＝∠GND，证出N、G、F、D四点共圆，由圆周角定理得出∠NFG＝∠NDG＝45°，由∠ANC＝∠AFC＝90°，得出A、N、F、C四点共圆，由圆周角定理得出∠ACN＝∠NFG＝45°，得出∠CHD＝90°，由直角三角形的性质得出DN＝

CD＝2，CN＝DN＝2，得出AC＝CN＝2；

（2）由（1）得：△ADH、△CGH是等腰直角三角形，由等腰直角三角形的性质即可得出结论．

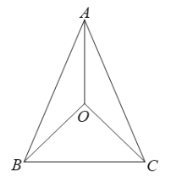
（1）解：延长CG交AD于N，连接NF，AC交DE于H，如图所示：

∵四边形ABCD是平行四边形，

∴AD∥BC，

∵GC⊥BC，∠DEC＝45°，

∴∠DGN＝∠CGE＝45°，GC⊥AD，

∴∠GND＝90°，

∴∠NDG＝45°，

∵AF⊥CD，

∴∠GFD＝90°＝∠GND，

∴N、G、F、D四点共圆，

∴∠NFG＝∠NDG＝45°，

又∵∠ANC＝∠AFC＝90°，

∴A、N、F、C四点共圆，

∴∠ACN＝∠NFG＝45°，

∴∠CHD＝45°＋45°＝90°，

∵CD＝4，∠DCG＝30°，

∴DN＝

CD＝2，CN＝DN＝2，

∴AC＝CN＝2；

（2）证明：由（1）得：△ADH、△CGH是等腰直角三角形，

∴AD＝HD＝（HG＋DG）＝HG＋DG＝CG＋DG．