题目内容
 如下网格图中,每个小三角形的边长都为1个单位,E是正△ABC内一点,以C为旋转中心,将△AEC沿顺时针方向旋转120°得到△A1E1C,再以C为旋转中心,将△AEC沿逆时针方向旋转60°得到△BE2C
如下网格图中,每个小三角形的边长都为1个单位,E是正△ABC内一点,以C为旋转中心,将△AEC沿顺时针方向旋转120°得到△A1E1C,再以C为旋转中心,将△AEC沿逆时针方向旋转60°得到△BE2C(1)试画出△A1E1C及△BE2C;
(2)直接说出△A1E1C和△BE2C有何对称关系?
(3)判断EE1,EE2,E1E2有何数量对称关系?
分析:(1)利用旋转的性质得出对应点坐标得出即可;
(2)利用图象以及旋转角度得出)△A1E1C和△BE2C关于C成中心对称;
(3)利用旋转的性质以及等边三角形的判定与性质得出△E2EE1是直角三角形,进而得出答案.
(2)利用图象以及旋转角度得出)△A1E1C和△BE2C关于C成中心对称;
(3)利用旋转的性质以及等边三角形的判定与性质得出△E2EE1是直角三角形,进而得出答案.
解答: 解:(1)如图所示:△A1E1C及△BE2C即为所求;
解:(1)如图所示:△A1E1C及△BE2C即为所求;
(2)△A1E1C和△BE2C关于C成中心对称;
(3)∵△AEC沿逆时针方向旋转60°得到△BE2C,
∴EC=CE2,∠ECE2=60°,
∴△ECE2是等边三角形,
∴∠EE2E1=∠E2EC=60°,
∵EC=E1C,∠ECE1=120°,
∴∠CEE1=∠CE1E=30°,
∴∠E2EE1=90°,
∴△E2EE1是直角三角形,
∴EE
+EE
=E1E
.
 解:(1)如图所示:△A1E1C及△BE2C即为所求;
解:(1)如图所示:△A1E1C及△BE2C即为所求;(2)△A1E1C和△BE2C关于C成中心对称;
(3)∵△AEC沿逆时针方向旋转60°得到△BE2C,
∴EC=CE2,∠ECE2=60°,
∴△ECE2是等边三角形,
∴∠EE2E1=∠E2EC=60°,
∵EC=E1C,∠ECE1=120°,
∴∠CEE1=∠CE1E=30°,
∴∠E2EE1=90°,
∴△E2EE1是直角三角形,
∴EE
2 2 |
2 1 |
2 2 |
点评:此题主要考查了图形的旋转的性质以及旋转变换,根据已知得出对应点位置是解题关键.

练习册系列答案
 活力课时同步练习册系列答案
活力课时同步练习册系列答案 学业测评一课一测系列答案
学业测评一课一测系列答案
相关题目


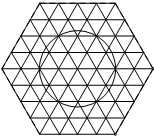
 如下网格图中,每个小三角形的边长都为1个单位,E是正△ABC内一点,以C为旋转中心,将△AEC沿顺时针方向旋转120°得到△A1E1C,再以C为旋转中心,将△AEC沿逆时针方向旋转60°得到△BE2C
如下网格图中,每个小三角形的边长都为1个单位,E是正△ABC内一点,以C为旋转中心,将△AEC沿顺时针方向旋转120°得到△A1E1C,再以C为旋转中心,将△AEC沿逆时针方向旋转60°得到△BE2C 所在圆的圆心D,并连接AD、CD。 (尺规作图,不写作法,保留作图痕迹)
所在圆的圆心D,并连接AD、CD。 (尺规作图,不写作法,保留作图痕迹)