Question

【题目】已知，在△ABC中，∠ABC=90°，AB=4，BC=3，若线段CD=2，且CD∥AB，则AD的长度等于 ．

Answer 1

【答案】 或3
【解析】解：分两种情况： ①如图1所示：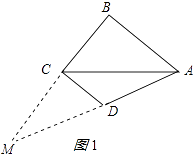

延长BC、AD交于点M，
∵CD∥AB，
∴△DCM∽△ABN，
∴ = = ，
∴CN=BC=3，AD═ AN，
∴BN=6，
∵∠ABC=90°，
∴AN= = =2 ，
∴AD= ；
②如图2所示：

设AD交BC于O，
∵CD∥AB，∠ABC=90°，
∴△COD∽△BOA，
∴ = ，
∵BC=3，
∴OC=1，OB=2，
∴OD= = ，OA= =2 ，
∴AD=OA+OD=3 ；
综上所述：AD的长度等于 或3 ；
所以答案是： 或3 ．
【考点精析】关于本题考查的勾股定理的概念，需要了解直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2才能得出正确答案．