题目内容
若α是Rt△ABC中的一个锐角,且sinα+cosα=m,sinαcosα=n,则m,n是怎样的关系?
考点:同角三角函数的关系
专题:
分析:利用完全平方公式以及sin2A+cos2A=1,进而求出即可.
解答:解:∵sinα+cosα=m,sinαcosα=n,
∴(sinα+cosα)2=sin2α+cos2α+2sinαcosα=1+2sinαcosα,
即m2=1+2n.
∴(sinα+cosα)2=sin2α+cos2α+2sinαcosα=1+2sinαcosα,
即m2=1+2n.
点评:此题主要考查了同角三角函数关系,利用完全平方公式得出是解题关键.

练习册系列答案
相关题目
下列说法正确的是( )
| A、+8的绝对值与-8的绝对值互为相反数 |
| B、数轴上原点两侧的两个点所对应的两个数的绝对值相等 |
| C、绝对值等于2的数是2 |
| D、既不是正数又不是负数的有理数的绝对值是0 |
下列运用等式性质变形,错误的是( )
| A、若a=b,则a-c=b-c | ||||
| B、若a=b,则-3a=-3b | ||||
C、若-2x=3,则x=-
| ||||
D、若m=n,则
|
下列方程中是关于x的一元二次方程的是( )
| A、x2-4x+3=0 |
| B、ax2+bx+c=0 |
| C、x2+x-2=0 |
| D、3x2-2xy-5y2=0 |
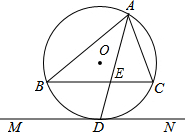 已知,△ABC内接于半径为5的⊙O,AD平分∠BAC,交直线BC于点E,交⊙O于点D.
已知,△ABC内接于半径为5的⊙O,AD平分∠BAC,交直线BC于点E,交⊙O于点D.