题目内容
【题目】如图,在![]() 中,
中,![]() 于
于![]() ,且
,且![]() .
.
(![]() )求证:
)求证:![]() .
.
(![]() )若
)若![]() ,
,![]() 于
于![]() ,
,![]() 为
为![]() 中点,
中点,![]() 与
与![]() ,
,![]() 分别交于点
分别交于点![]() ,
,![]() .
.
①判断线段![]() 与
与![]() 相等吗?请说明理由.
相等吗?请说明理由.
②求证:![]() .
.

【答案】见解析
【解析】试题分析:(1)根据SAS证明△ABE≌△CBE,即可得结论;(2)①BH=AC,根据已知条件求出∠BCD=∠ABC,∠ABE=∠DCA,推出DB=CD,根据ASA证出△DBH≌△DCA,即可得结论;②连接CG,AG,根据AB=BC,BE⊥AC,可得BE垂直平分AC,根据线段垂直平分线的性质可得AG=CG,再由F点是BC的中点,DB=DC,可得DF垂直平分BC,所以BG=CG,即可得AG=BG,在Rt△AEG中,由勾股定理即可推出答案.
试题解析:
(![]() )证明:在
)证明:在![]() 与
与![]() 中,
中,
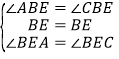 ,
,
∴![]() ≌
≌![]() ,
,
∴![]() .
.
(![]() )①
)①![]() ,
,
理由:∵![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,
在![]() 与
与![]() 中,
中,
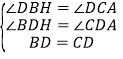 ,
,
∴![]() ≌
≌![]() ,
,
∴![]() .
.
②证明:如图,连接![]() ,
,![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() 垂直平分
垂直平分![]() ,
,
∴![]() ,
,
∵![]() 点是
点是![]() 的中点,
的中点,![]() ,
,
∴![]() 垂直平分
垂直平分![]() ,
,
∴![]() ,
,
∴![]() ,
,
在![]() 中,
中,![]() ,
,
∴![]() .
.


练习册系列答案
相关题目