题目内容
5.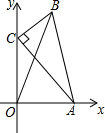 如图,在△ABC中,∠C=90°,AC=4,BC=2,点A、C分别在x轴、y轴上,当点A在x轴上运动时,点C随之在y轴上运动,在运动过程中,点B到原点的最大距离是( )
如图,在△ABC中,∠C=90°,AC=4,BC=2,点A、C分别在x轴、y轴上,当点A在x轴上运动时,点C随之在y轴上运动,在运动过程中,点B到原点的最大距离是( )| A. | 2$\sqrt{2}$+2 | B. | 2$\sqrt{5}$ | C. | 2$\sqrt{6}$ | D. | 6 |
分析 在运动过程中,点O、点B到AC的中点D的距离不变,根据三角形两边之和大于第三边,可知B、D、O在一条直线上时,点B到原点O的最大可得出答案.
解答 解:取AC的中点D,连接OD、DB,
∵OB≤OD+BD,
∴当O、D、B三点共线时OB取得最大值,
∵D是AC中点,
∴OD=$\frac{1}{2}$AC=2,
在Rt△BCD中,BD=$\sqrt{B{C}^{2}+C{D}^{2}}$=$\sqrt{{2}^{2}+{2}^{2}}$=2$\sqrt{2}$,OD=$\frac{1}{2}$AC=2,
∴点B到原点O的最大距离为2+2$\sqrt{2}$,
故选:A.
点评 此题主要考查了两点间的距离,以及勾股定理的应用,在解题过程中应用三角形两边之和大于第三边,正确判断当三点共线时距离最大是解决本题的关键.

练习册系列答案
相关题目
20.下列等式成立的是( )
| A. | 6÷(-$\frac{1}{4}$)×4=6×(-4)×4 | B. | 6÷(-$\frac{1}{4}$)×4=6×(-$\frac{1}{4}$)×4 | C. | 6÷(-$\frac{1}{4}$)×4=6÷(-$\frac{1}{4}$×4) | D. | 6÷(-$\frac{1}{4}$)×4=6×(-4)÷4 |
10. 如图,正方形ABCD的四个顶点分别在四条平行线l1,l2,l3,l4上,AD,BC边分别与l2,l3相交于点F,E,这四条直线中相邻两条之间的距离依次为a,b,c(a>0,b>0,c>0),且AB边于直线l2的夹角为α,则下列结论错误的是( )
如图,正方形ABCD的四个顶点分别在四条平行线l1,l2,l3,l4上,AD,BC边分别与l2,l3相交于点F,E,这四条直线中相邻两条之间的距离依次为a,b,c(a>0,b>0,c>0),且AB边于直线l2的夹角为α,则下列结论错误的是( )
 如图,正方形ABCD的四个顶点分别在四条平行线l1,l2,l3,l4上,AD,BC边分别与l2,l3相交于点F,E,这四条直线中相邻两条之间的距离依次为a,b,c(a>0,b>0,c>0),且AB边于直线l2的夹角为α,则下列结论错误的是( )
如图,正方形ABCD的四个顶点分别在四条平行线l1,l2,l3,l4上,AD,BC边分别与l2,l3相交于点F,E,这四条直线中相邻两条之间的距离依次为a,b,c(a>0,b>0,c>0),且AB边于直线l2的夹角为α,则下列结论错误的是( )| A. | a=c | B. | 当a=b=c时,四边形BEDF是菱形 | ||
| C. | $\frac{AF}{AB}$=$\frac{a}{a+b}$ | D. | 正方形ABCD面积为(a+b)2+c2 |
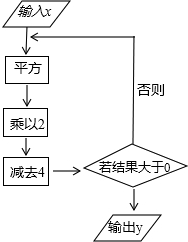 根据如图所示的程序计算.
根据如图所示的程序计算.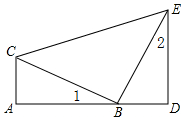 如图,已知A、B、D在同一条直线上,∠A=∠D=90°,AC=BD,∠1=∠2.
如图,已知A、B、D在同一条直线上,∠A=∠D=90°,AC=BD,∠1=∠2.