题目内容
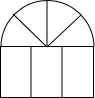 某建筑物的窗口如图所示,它的上半部是半圆,下半部是矩形,制造窗框的材料总长(图中所有黑线的长度和)为15m,当半圆的半径为多少时,窗户通过的光线最多?此时,窗户的面积是多少(结果精确到0.01m)?
某建筑物的窗口如图所示,它的上半部是半圆,下半部是矩形,制造窗框的材料总长(图中所有黑线的长度和)为15m,当半圆的半径为多少时,窗户通过的光线最多?此时,窗户的面积是多少(结果精确到0.01m)?
分析:先设圆半径、矩形的宽和窗户的面积,再根据给出的已知条件列出它们的函数关系式,根据函数关系式来求最大值.
解答: 解:设半圆的半径为xm,矩形的宽为ym,窗户的面积为Sm2.
解:设半圆的半径为xm,矩形的宽为ym,窗户的面积为Sm2.
∵材料的总长为15m,
∴4y+7x+πx=15,
∴y=
(15-7x-πx),
从而S=2x•
(15-7x-πx)+
πx2=-3.5x2+7.5x.
∵-3.5<0,
∴S有最大值,
当x=-
=
时,
S最大=
≈4.02.
答:当半圆的半径约为l.07m时,窗户通过的光线最多,此时窗户的面积约为4.02m2.
 解:设半圆的半径为xm,矩形的宽为ym,窗户的面积为Sm2.
解:设半圆的半径为xm,矩形的宽为ym,窗户的面积为Sm2.∵材料的总长为15m,
∴4y+7x+πx=15,
∴y=
| 1 |
| 4 |
从而S=2x•
| 1 |
| 4 |
| 1 |
| 2 |
∵-3.5<0,
∴S有最大值,
当x=-
| 7.5 |
| 2×(-3.5) |
| 15 |
| 14 |
S最大=
| -(7.5)2 |
| 4×(-3.5) |
答:当半圆的半径约为l.07m时,窗户通过的光线最多,此时窗户的面积约为4.02m2.
点评:本题主要考查二次函数在实际生活中的应用,其中涉及圆的周长、矩形周长的计算和求最值的问题.

练习册系列答案
 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案
相关题目



 m,则水流落地点B离墙的距离OB是
m,则水流落地点B离墙的距离OB是