题目内容
13．
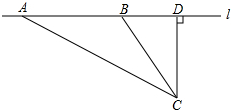校车安全是近几年社会关注的重大问题．某数学活动小组设计了如下检测校车速度的实验：先在公路旁边选取一点C，再在笔直的车道l上确定点D，使CD与l垂直，测得CD=30米，在l上点D的同侧取点A、B，使∠CAD=30°，∠CBD=60°．已知本路段对校车限速为40千米/小时，若测得某辆校车从A到B用时3秒，这辆校车是否超速？说明理由．（参考数据：$\sqrt{3}$=1.73，$\sqrt{2}$=1.41）
分析 根据CD=30，∠CAD=30°，∠CBD=60°可以利用三角函数计算出AD和BD，然后即可算出AB的长；根据速度=路程÷时间算出速度，再与40千米/小时进行比较即可得到答案．
解答 解?∵CD=30，∠CAD=30°，∠CBD=60°，
∴AD=30$\sqrt{3}$，BD=10$\sqrt{3}$，?
∴AB=AD-BD=20$\sqrt{3}$≈34.64（米）；
∵汽车从A到B用时3秒，
?速度为36.64÷3=12.2（米/秒），??
∵12.2×3600=49320，?
∴该车速度为49.32千米/小时
∵大于40千米/小时，?
∴此校车在AB路段超速．
点评 此题主要考查了勾股定理的应用，关键是利用三角函数计算出AD、BD的长度，难度不大．
练习册系列答案
相关题目
18．
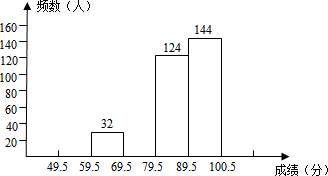某县九年级有15000名学生参加安全应急预案知识竞赛活动，为了了解本次知识竞赛的成绩分布情况，从中抽取了400名学生的得分（得分取正整数，满分100分）进行统计：
频率分布表
请结合图表完成下列问题：
（1）表中的a=80、b=0.05、c=0.31．
（2）请把频数分布直方图补充完整；
（3）若将得分转化为等级，规定得分低于59.5分评为“D”，59.5～69.5分评为“C”，69.5～89.5分评为“B”，89.5～100.5分评为“A”，这次15000名学生中约有多少人评为“B”？
某县九年级有15000名学生参加安全应急预案知识竞赛活动，为了了解本次知识竞赛的成绩分布情况，从中抽取了400名学生的得分（得分取正整数，满分100分）进行统计：频率分布表
| 分 组 | 频 数 | 频 率 |
| 49.5～59.5 | 20 | b |
| 59.5～69.5 | 32 | 0.08 |
| 69.5～79.5 | a | 0.20 |
| 79.5～89.5 | 124 | c |
| 89.5～100.5 | 144 | 0.36 |
| 合 计 | 400 | 1 |
（1）表中的a=80、b=0.05、c=0.31．
（2）请把频数分布直方图补充完整；
（3）若将得分转化为等级，规定得分低于59.5分评为“D”，59.5～69.5分评为“C”，69.5～89.5分评为“B”，89.5～100.5分评为“A”，这次15000名学生中约有多少人评为“B”？
5．下列运算正确的是（ ）
| A． | 2x2•x3=2x5 | B． | （x-2）2=x2-4 | C． | x2+x3=x5 | D． | （x3）4=x7 |
2．下列计算正确的是（ ）
| A． | 2-3=1 | B． | a2+2a2=3a4 | C． | 3×（-1）2=3 | D． | -|-3|=3 |