题目内容
 如图所示,花园边墙上有一宽为1m的矩形门ABCD,量得门框对角线AC的长为2m.现准备打掉部分墙体,使其变为以AC为直径的圆弧形门,问要打掉墙体的面积是多少?
如图所示,花园边墙上有一宽为1m的矩形门ABCD,量得门框对角线AC的长为2m.现准备打掉部分墙体,使其变为以AC为直径的圆弧形门,问要打掉墙体的面积是多少?(精确到0.1m2,π≈3.14,
| 3 |
分析:设矩形外接圆的圆心为O,作OE⊥BC,垂足为E,连接AC,BD.有AC=2,BC=1,可求AB=
,且可得到∠BAC=30°,于是∠ACB=60°,可以知道△OBC是等边三角形,因此OE=
.打掉墙体的面积=S⊙O-S矩形-S扇形OBC+S△OBC,计算各部分的面积就可求出.
| 3 |
| ||
| 2 |
解答: 解:设矩形外接圆的圆心为O,作OE⊥BC,垂足为E,连接AC,BD.
解:设矩形外接圆的圆心为O,作OE⊥BC,垂足为E,连接AC,BD.
∵矩形ABCD的AC=2m,BC=1m,
∴∠BAD=∠BCD=90°,AB=
=
,
∴AC、BD均为⊙O的直径,
∴⊙O的半径R=
=1(m),
∵BO=CO=BC=1m,
∴△OBC是等边三角形,
∴∠BOC=60°.在Rt△OEB中,OB=1(m),∠OBE=60°,sin∠OBE=
,
∴OE=OB•sin∠OBE=
(m),
应打掉的墙体面积为S=S⊙O-S矩形ABCD-S扇形OBC+S△OBC
=π×12-1×
-
+
×1×
≈1.3m2.
 解:设矩形外接圆的圆心为O,作OE⊥BC,垂足为E,连接AC,BD.
解:设矩形外接圆的圆心为O,作OE⊥BC,垂足为E,连接AC,BD.∵矩形ABCD的AC=2m,BC=1m,
∴∠BAD=∠BCD=90°,AB=
| 22-12 |
| 3 |
∴AC、BD均为⊙O的直径,
∴⊙O的半径R=
| AC |
| 2 |
∵BO=CO=BC=1m,
∴△OBC是等边三角形,
∴∠BOC=60°.在Rt△OEB中,OB=1(m),∠OBE=60°,sin∠OBE=
| OE |
| OB |
∴OE=OB•sin∠OBE=
| ||
| 2 |
应打掉的墙体面积为S=S⊙O-S矩形ABCD-S扇形OBC+S△OBC
=π×12-1×
| 3 |
| 60π×12 |
| 360 |
| 1 |
| 2 |
| ||
| 2 |
点评:本题考查了矩形的性质,扇形、矩形、三角形、圆的面积公式及勾股定理的使用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图所示,花园边墙上有一宽为1m的矩形门ABCD,量得门框对角线AC的长为2m.现准备打掉部分墙体,使其变为以AC为直径的圆弧形门,问要打掉墙体的面积是多少?
如图所示,花园边墙上有一宽为1m的矩形门ABCD,量得门框对角线AC的长为2m.现准备打掉部分墙体,使其变为以AC为直径的圆弧形门,问要打掉墙体的面积是多少? ≈1.73)
≈1.73)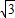 ≈1.73)
≈1.73)
 ≈1.73)
≈1.73)
 ≈1.73)
≈1.73)