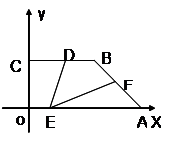题目内容
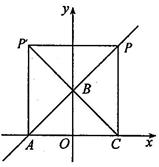
如图,在平面直角坐标系中,O是坐标原点,点A的坐标为(-4,0),点B的坐标为(0,b)(b>0). P是直线AB上的一个动点,作PC⊥x轴,垂足为C.记点P关于y轴的对称点为P'(点 P'不在y轴上),连结P P', P'A,P'C.设点P的横坐标为a.

(1) 当b=3时,求直线AB的解析式;
(2) 在(1)的条件下,若点P'的坐标是(-1,m),求m的值;
(3) 若点P在第一像限,是否存在a ,使△P'CA为等腰直角三角形?若存在,请求出所有满足要求的a的值;若不存在,请说明理由.

(1) 当b=3时,求直线AB的解析式;
(2) 在(1)的条件下,若点P'的坐标是(-1,m),求m的值;
(3) 若点P在第一像限,是否存在a ,使△P'CA为等腰直角三角形?若存在,请求出所有满足要求的a的值;若不存在,请说明理由.
解: (1)设直线AB的解析式为y=kx+3,
把x=-4,y=0代人上式,得-4k+3=0,
∴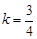 , ∴
, ∴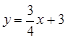
(2)由已知得点P的坐标是(1,m),
∴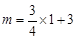 ,∴
,∴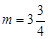 .
.
(3) 以下分三种情况讨论.
i)若∠AP'C= 90°,P'A= P'C(如图1),过点P'作P'H⊥x轴于点'H,
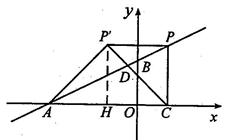
∴PP'=CH=AH=P'H =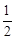 AC,
AC,
∴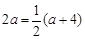 ,∴
,∴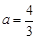 .
.
ii)若∠P'AC=90°,P'A= CA(如图2),
则PP'=AC,∴2a=a+4,∴ a=4.
iii)若∠P'CA =90°,则点P',P都在第一象限,
这与条件矛盾,
∴△P'CA不可能是以C为直角顶点的等腰直角三角形.
把x=-4,y=0代人上式,得-4k+3=0,
∴
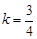 , ∴
, ∴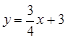
(2)由已知得点P的坐标是(1,m),
∴
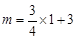 ,∴
,∴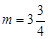 .
.(3) 以下分三种情况讨论.
i)若∠AP'C= 90°,P'A= P'C(如图1),过点P'作P'H⊥x轴于点'H,

∴PP'=CH=AH=P'H =
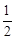 AC,
AC,∴
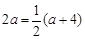 ,∴
,∴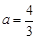 .
.ii)若∠P'AC=90°,P'A= CA(如图2),

则PP'=AC,∴2a=a+4,∴ a=4.
iii)若∠P'CA =90°,则点P',P都在第一象限,
这与条件矛盾,
∴△P'CA不可能是以C为直角顶点的等腰直角三角形.
(1)利用待定系数法即可求得函数的解析式;
(2)把(-1,m)代入函数解析式即可求得m的值;可以证明△PP′D∽△ACD,根据相似三角形的对应边的比相等,即可求解;
(3)点P在第一像限,若使△P'CA为等腰直角三角则∠AP′C=90°或∠P′AC=90°或∠P′CA=90°就三种情况分别讨论求出出所有满足要求的a的值即可
(2)把(-1,m)代入函数解析式即可求得m的值;可以证明△PP′D∽△ACD,根据相似三角形的对应边的比相等,即可求解;
(3)点P在第一像限,若使△P'CA为等腰直角三角则∠AP′C=90°或∠P′AC=90°或∠P′CA=90°就三种情况分别讨论求出出所有满足要求的a的值即可

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目

 ,y1)、N(
,y1)、N( ,y2)、P(
,y2)、P( ,y3)三点都在函数
,y3)三点都在函数 (
( )的图象上,则yl、y2、y3的大小关系是( )
)的图象上,则yl、y2、y3的大小关系是( ) 和点
和点 关于原点对称,已知点
关于原点对称,已知点 ,
, ),那么点
),那么点 ,
, );
);  .(
.( .(
.(
 是一个无理数
是一个无理数 的自变量的取值范围是x>﹣1
的自变量的取值范围是x>﹣1