题目内容
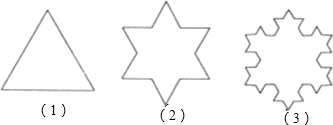
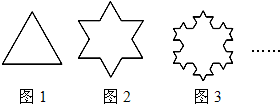
如图，设有一个边长为1的正三角形（图1），将每条边三等分，以中间的线段为一边向外做正三角形，并去掉中间的线段后得到图2，称为第1次“生长”；再将图2的每条边三等分，并重复上述过程，得到图3，称为第2次“生长”；…．则第2次“生长”后的图形的周长等于
，第n次“生长”后的图形的周长等于
．
| 16 |
| 3 |
| 16 |
| 3 |
| 4n |
| 3n-1 |
| 4n |
| 3n-1 |
分析：注意首先根据前面几个图形找到相邻周长之间的关系．再进一步得到和第一个图形的周长之间的关系．
解答：解：观察图形发现：第一个图形的周长是3，经过第一次生长的图形的周长是3+3×
=3×
．
经过第二次生长的图形的周长是3×
+3×4×
×
=3×（
）2=
，
以此类推，则经过第n次生长的第n个图形的周长是3×（
）n=
．
故答案为：
，
．
| 1 |
| 3 |
| 4 |
| 3 |
经过第二次生长的图形的周长是3×
| 4 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| 4 |
| 3 |
| 16 |
| 3 |
以此类推，则经过第n次生长的第n个图形的周长是3×（
| 4 |
| 3 |
| 4n |
| 3n-1 |
故答案为：
| 16 |
| 3 |
| 4n |
| 3n-1 |
点评：此题主要考查了图形变化规律，根据题意得出第一、第二图形的周长，找出规律是解答此题的关键．
练习册系列答案
相关题目
