Question

如图所示，四边形ABCD中，AB=1，BC=2，CD=2，AD=3，且AB⊥BC．求证：AC⊥CD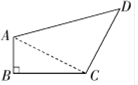

Answer 1

先根据勾股定理求得AC的长，再根据勾股定理的逆定理即可作出判断.

试题分析：∵AB=1，BC=2，AB⊥BC
∴
∵CD=2，AD=3
∴，即
∴△ACD为直角三角形
∴AC⊥CD
点评：解答本题的关键是熟练掌握勾股定理的逆定理：若一个三角形的两边长的平方和等于第三边的平方，则这个三角形的直角三角形.