题目内容
如图，P为∠AOB内一点，OA=OB，且△OPA与△OPB面积相等，求证∠AOP=∠BOP.
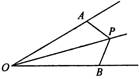
【答案】
证明见解析
【解析】本题主要考查了三角形的面积以及角平分线上一点到角两边距离相等的性质问题. 可分别作OA、OB边上的高，由面积相等及OA=OB，可得其高相等，即PM=PN，进而结论得证
作PM⊥OA交OA延长线于M PN⊥OB交OB延长线于N.
∵S△OPA=S△OPB ∴
OA·PM=OB·PN OA=OB ∴PM=PN ∴∠AOP=∠BOP
练习册系列答案
科学实验活动册系列答案
相关题目
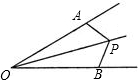如图，P为∠AOB内一点，OA=OB，且△OPA与△OPB面积相等，求证：∠AOP=∠BOP．
如图，P为∠AOB内一点，P1，P2分别是P关于OA、OB的对称点，P1P2交OA于M，交OB于 N，若P1P2=8cm，则△PMN的周长是（ ）cm．
如图，P为∠AOB内的一点，分别作出点P关于OA、OB的对称点P1、P2，连结P1、P2，交OA于M，交OB于N，若P1P2=13cm，求△MNP的周长？
，
分别是P关于OA、OB的对称点，