Question

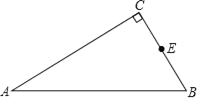
【题目】如图1，△ABC中，∠A＝30°，点P从点A出发以2cm/s的速度沿折线A→C→B运动，点Q从点A出发以vcm/s的速度沿AB运动，P，Q两点同时出发，当某一点运动到点B时，两点同时停止运动．设运动时间为x（s），△APQ的面积为y（cm2），y关于x的函数图象由C1，C2两段组成，如图2所示，有下列结论：①v＝1；②sinB＝；③图象C2段的函数表达式为y＝﹣x2+x；④△APQ面积的最大值为8，其中正确有（　　）

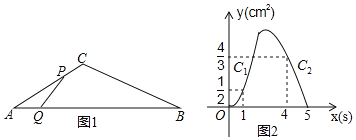
A.①②B.①②④C.①③④D.①②③④

Answer 1

【答案】A

【解析】

①根据题意列出y＝ APAQsinA，即可解答

②根据图像可知PQ同时到达B，则AB＝5，AC+CB＝10，再代入即可

③把sinB＝，代入解析式即可

④根据题意可知当x＝﹣时，y最大＝

①当点P在AC上运动时，y＝ APAQsinA＝×2xvx＝vx2，

当x＝1，y＝时，得v＝1，

故此选项正确；

②由图象可知，PQ同时到达B，则AB＝5，AC+CB＝10，

当P在BC上时y＝x（10﹣2x）sinB，

当x＝4，y＝ 时，代入解得sinB＝ ，

故此选项正确；

③∵sinB＝，

∴当P在BC上时y＝x（10﹣2x）×＝﹣x2+ x，

∴图象C2段的函数表达式为y＝﹣x2+x，

故此选项不正确；

④∵y＝﹣x2+x，

∴当x＝﹣时，y最大＝ ，

故此选项不正确；

故选A．