题目内容
在Rt![]() 中,
中,![]() ,
,![]() ,
,![]() ,点P是AB边上任意一点,直线PE⊥AB,与边AC或BC相交于点E.点M在线段AP上,点N在线段BP上,且PM=PN,
,点P是AB边上任意一点,直线PE⊥AB,与边AC或BC相交于点E.点M在线段AP上,点N在线段BP上,且PM=PN,![]() .
.

1.(1)如图①,当点E与点C重合时,求MP的长;
2.(2)设![]() ,△ENB的面积为y,求y与x的函数关系式,并求出当x取何值时,y有最大值,最大值是多少?
,△ENB的面积为y,求y与x的函数关系式,并求出当x取何值时,y有最大值,最大值是多少?
1.解:(1)∵在Rt![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,
∴![]() . …………………………1分
. …………………………1分
由面积公式可得  .
.
∴![]() .……………………………………2分
.……………………………………2分
∵PE⊥AB,![]() ,
,
∴![]()
2. (2)分两种情况考虑:
(2)分两种情况考虑:
①当点![]() 在线段AC上时,如图②,
在线段AC上时,如图②,
在Rt△AEP和Rt△ABC中,
∵![]() ,
,![]() ,
,
∴△APE∽△ACB.
∴![]() ,即
,即![]() ,
,
∴![]() .
.
∵![]() ,
,
∴![]() .
.
∴![]() .
.
∴![]() .………………4分
.………………4分
当点E与点C重合时,![]() .
.
∴自变量x的取值范围是:![]() .…………………………………5分
.…………………………………5分
 ②当点
②当点![]() 在线段BC上时,如图③,
在线段BC上时,如图③,
在Rt△BPE和Rt△BCA中,
∵![]() ,
,![]() ,
,
∴△BPE∽△BCA.
∴![]() ,即
,即![]() ,
,
∴![]() .
.
∵![]() ,
,
∴![]() .
.
∴![]() .
.
∴![]() .
.
y与x的函数关系式为 ……………6分
……………6分
当点![]() 在线段AC上时,
在线段AC上时,![]() ,
,
此时,当![]() 时,y有最大值为
时,y有最大值为![]() .
.
而当点![]() 在线段BC上时,y的最大值为点E与点C重合时,显然没有
在线段BC上时,y的最大值为点E与点C重合时,显然没有![]() 大.
大.
∴当![]() 时,y有最大值,最大值为
时,y有最大值,最大值为![]() .
.
解析:略

练习册系列答案
 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目
 中,∠F="90°,点B、C分别在AD、FD上,以AB为直径的半圆O" 过点C,
中,∠F="90°,点B、C分别在AD、FD上,以AB为直径的半圆O" 过点C, ,且点E恰好落在直径AB上.
,且点E恰好落在直径AB上.
 中,
中, ,
, ,
, ,点
,点 在斜边
在斜边 上,分别作
上,分别作 于
于 ,
, 于
于 ,设
,设 ,
, .
.
 与
与 之间的函数关系,并求出
之间的函数关系,并求出 的面积为
的面积为 ,试求
,试求 中,
中, ,
, ,若点
,若点 是
是 =_______
=_______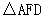 中,∠F=90°,点B、C分别在AD、FD上,以AB为直径的半圆O
过点C,
中,∠F=90°,点B、C分别在AD、FD上,以AB为直径的半圆O
过点C, ,且点E恰好落在直径AB上.
,且点E恰好落在直径AB上.