题目内容
12.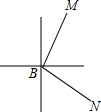 如图,在B港有甲、乙两艘渔船,若甲船沿北偏东30°的方向以每小时8海里速度前进,乙船沿南偏东60°的方向以每小时6海里速度前进,两小时后,甲船到M岛,乙船到N岛,求M岛到N岛的距离.
如图,在B港有甲、乙两艘渔船,若甲船沿北偏东30°的方向以每小时8海里速度前进,乙船沿南偏东60°的方向以每小时6海里速度前进,两小时后,甲船到M岛,乙船到N岛,求M岛到N岛的距离.
分析 根据条件可以证得△BMN是直角三角形,求得BN与BM的长,根据勾股定理即可求得MN的长.
解答 解:根据条件可知:BM=2×8=16(海里),BN=2×6=12(海里).
∵∠MBN=180°-60°-30°=90°,
∴△BMN是直角三角形,
∴MN=$\sqrt{B{M}^{2}+B{N}^{2}}$=$\sqrt{1{2}^{2}+1{6}^{2}}$=20(海里)
答:M岛与N岛之间的距离是20海里.
点评 本题主要考查了勾股定理,正确证明△BMN是直角三角形是解决本题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
4.下列事件中,不确定事件是( )
| A. | a是实数,且|a|≥0 | B. | $\frac{1}{2}$+$\frac{x-1}{5}$=0不是分式方程 | ||
| C. | 三角形内角和等于360° | D. | a是实数,a0=1 |
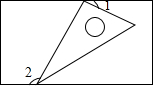 如图,将一个含有30°角的直角三角形的两个顶点放在一个矩形的对边上,若∠1=35°,则∠2=125°.
如图,将一个含有30°角的直角三角形的两个顶点放在一个矩形的对边上,若∠1=35°,则∠2=125°.