题目内容
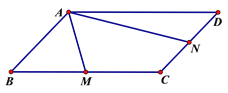
【题目】如图，在平行四边形ABCD中，M、N分别为BC、CD的中点，AM=1，AN=2，∠MAN=60°则AB的长为____________.
【答案】
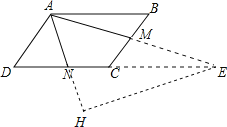
【解析】首先延长DC和AM交于E，过点E作EH⊥AN于点H，易证△ABM≌△ECM，则AM=EM=1，AN=2，且∠MAN=60°，求得AH，NH与EH的长，从而求得NE的长，则可求得答案.
解：（解法一）延长DC和AM交于E，过点E作EH⊥AN于点H，
∵ABCD为平行四边形
∴AB∥CE，
∴∠BAM=∠MEC，∠ABM=∠ECM，
∵M为BC的中点，
∴BM=MC，
∴△ABM≌△ECM，
∴AB=CD=CE，AM=EM=2，
∵N为DC的中点，
∴NE=3NC=
AB，即AB=
NE，
∵AN=2，AE=2AM=4，且∠MAN=60°，
∴∠AEH=30°，
∴AH=
AE=2，
∴EH=
，
∴NH=AH-AN=2-1=1，
∴EN=
，
∴AB=
.
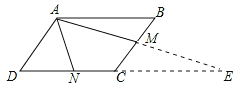
解法二：延长DC和AM交于E，根据平行四边形的性质可得出∠BAM=∠MEC，∠ABM=∠ECM，可证明△ABM≌△ECM，则AM=EM=2，由N为边DC的中点，得NR=3NC=1.5AB，AB=
NE，由余弦定理可解得EN，从而得出AB即可.
解：延长DC和AM交于E，
∵ABCD为平行四边形
∴AB∥CE，
∴∠BAM=∠MEC，∠ABM=∠ECM，
∵M为BC的中点，
∴BM=MC，
∴△ABM≌△ECM，
∴AB=CD=CE，AM=EM=2，
∵N为DC的中点，
∴NE=3NC=1.5AB即AB=
NE，
∵AN=2，AE=2AM=4，且∠MAN=60°，
由余弦定理EN2=AE2+AN2-2AE×ANcos60°=16+1-2×4×
=13，
∴EN=
,
∴AB=
.
故答案为： 
.
“点睛”本题考查了平行线的性质、勾股定理以及三角形的中位线定理，是中考常见的题型，难度偏大.
