题目内容
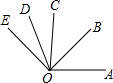 如图,OB是∠AOC的角平分线,OD是∠COE的角平分线,∠AOE=140°,∠COD=30°,则∠AOB=
如图,OB是∠AOC的角平分线,OD是∠COE的角平分线,∠AOE=140°,∠COD=30°,则∠AOB=
- A.35°
- B.40°
- C.45°
- D.50°
B
分析:根据角平分线的定义求得∠COB+∠DOC=70°;然后由已知条件和图示求得∠AOB=∠BOC=40°.
解答:∵OB是∠AOC的平分线,OD是∠COE的平分线,
∴∠COB+∠DOC= ∠AOE=
∠AOE= ×140°=70°;
×140°=70°;
又∵∠COD=30°,
∴∠AOB=∠BOC=40°.
故选B.
点评:本题考查了角平分线的定义、角的计算.此题属于基础题,只要找准角与角间的和差关系,即可求得正确答案.
分析:根据角平分线的定义求得∠COB+∠DOC=70°;然后由已知条件和图示求得∠AOB=∠BOC=40°.
解答:∵OB是∠AOC的平分线,OD是∠COE的平分线,
∴∠COB+∠DOC=
 ∠AOE=
∠AOE= ×140°=70°;
×140°=70°;又∵∠COD=30°,
∴∠AOB=∠BOC=40°.
故选B.
点评:本题考查了角平分线的定义、角的计算.此题属于基础题,只要找准角与角间的和差关系,即可求得正确答案.

练习册系列答案
相关题目
 25、如图,OB是∠AOC的平分线,OC是∠AOD的平分线,∠COD=76°,求∠BOD的度数.
25、如图,OB是∠AOC的平分线,OC是∠AOD的平分线,∠COD=76°,求∠BOD的度数. 如图,OB是∠AOC的角平分线,OD是∠COE的角平分线.∠DOE=
如图,OB是∠AOC的角平分线,OD是∠COE的角平分线.∠DOE= 12、如图,OB是∠AOC的平分线,OD是∠COE的平分线,若∠AOC=70°,∠COE=40°,那么∠BOD=
12、如图,OB是∠AOC的平分线,OD是∠COE的平分线,若∠AOC=70°,∠COE=40°,那么∠BOD= 如图,OB是∠AOC的平分线,OD是∠COE的平分线,∠AOE=150°,∠AOB=35°,求∠AOD的度数.
如图,OB是∠AOC的平分线,OD是∠COE的平分线,∠AOE=150°,∠AOB=35°,求∠AOD的度数. 如图,OB是∠AOC的平分线,OD是∠COE的平分线.
如图,OB是∠AOC的平分线,OD是∠COE的平分线.