题目内容
 如图,△ABC中,∠ACB=90°,AC=12,BC=16.点P从A点出发沿A-C-B路径
如图,△ABC中,∠ACB=90°,AC=12,BC=16.点P从A点出发沿A-C-B路径向终点运动,终点为B点;点Q从B点出发沿B-C-A路径向终点运动,终点为A点.点P和Q分别以2和6的运动速度同时开始运动,两点都要到相应的终点时才能停止运动,在某时刻,分别过P和Q作PE⊥l于E,QF⊥l于F.
问:点P运动多少时间时,△PEC与QFC全等?请说明理由.
考点:全等三角形的判定
专题:动点型
分析:推出CP=CQ,①P在AC上,Q在BC上,推出方程6-t=8-3t,②P、Q都在AC上,此时P、Q重合,得到方程6-t=3t-8,Q在AC上,③P在BC上,Q在AC时,此时不存在,④当Q到A点,与A重合,P在BC上时,求出即可得出答案.
解答:解:∵△PEC≌△QFC,∴斜边CP=CQ,有四种情况:
①P在AC上,Q在BC上,
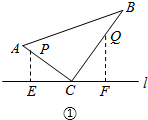 ,
,
CP=12-2t,CQ=16-6t,
∴12-2t=16-6t,
∴t=1;
②P、Q都在AC上,此时P、Q重合,
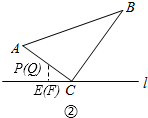
∴CP=12-2t=6t-16,
∴t=3.5;
③P到BC上,Q在AC时,此时不存在;
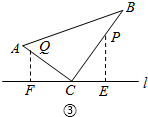
理由是:16÷6×2<12,Q到AC上时,P点也在AC上;
④当Q到A点(和A重合),P在BC上时,
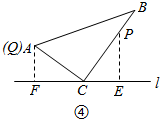
∵CP=CQ=AC=12.CP=12-2t,
∴2t-12=12,
∴t=12符合题意;
答:点P运动1或3.5或12时,△PEC与△QFC全等.
①P在AC上,Q在BC上,
 ,
,CP=12-2t,CQ=16-6t,
∴12-2t=16-6t,
∴t=1;
②P、Q都在AC上,此时P、Q重合,

∴CP=12-2t=6t-16,
∴t=3.5;
③P到BC上,Q在AC时,此时不存在;

理由是:16÷6×2<12,Q到AC上时,P点也在AC上;
④当Q到A点(和A重合),P在BC上时,

∵CP=CQ=AC=12.CP=12-2t,
∴2t-12=12,
∴t=12符合题意;
答:点P运动1或3.5或12时,△PEC与△QFC全等.
点评:本题主要考查对全等三角形的性质,解一元一次方程等知识点的理解和掌握,能根据题意得出方程是解此题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
菱形具有而矩形不具有的性质是( )
| A、内角和为360° |
| B、对角线平分一组对角 |
| C、对角相等 |
| D、对角线互相平分 |
 如图,∠1=∠2,∠C=∠D.求证:∠A=∠F.
如图,∠1=∠2,∠C=∠D.求证:∠A=∠F. 如果抛物线m的顶点在抛物线n上,同时抛物线n的顶点在抛物线m上,那么我们就称抛物线m与n为交融抛物线.
如果抛物线m的顶点在抛物线n上,同时抛物线n的顶点在抛物线m上,那么我们就称抛物线m与n为交融抛物线.