Question

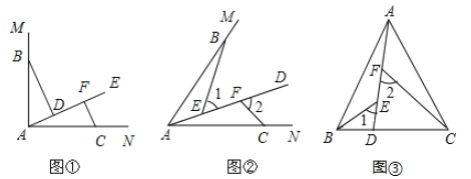
【题目】（1）如图①，，射线在这个角的内部，点、分别在的边、上，且，于点，于点．求证：；

（2）如图②，点、分别在的边、上，点、都在内部的射线上，、分别是、的外角．已知，且．求证：；

（3）如图③，在中，，．点在边上，，点、在线段上，．若的面积为15，求与的面积之和．

Answer 1

【答案】（1）详见解析；（2）详见解析；（3）5.

【解析】

（1）先利用相同角的余角相等得到，再通过“角角边”证明即可；

（2）根据题意易得，利用三角形的外角性质与等量代换可得，再通过“角角边”证明即可；

（3）同理（2）可得，因为，所以，则.

（1）解：证明：∵，

即，

又∵，，

∴，

，

∴，

在和中，

∵，

∴.

（2）解：证明：∵，

∴，

又∵，

，

，

∴，

在和中，

∵，

∴.

（3）解：由（2）知，

∵，

∴，

∵，

∴

，

，

.