题目内容
已知：如图，在正方形ABCD中，P是BC上的点，且BP=3PC，Q是CD的中点．△ADQ与△QCP是否相似？
为什么？
解：△ADQ∽△PCQ
∵BP=3PC，
∴CP=
BC=CD，
∵Q是CD的中点，
∴CQ=DQ=
AD．
∴
=
=，
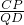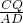又∵∠C=∠D．
∴△ADQ∽△QCP．
分析：正方形的四边相等，两个三角形的两组对应边成比例，夹角相等的两个三角形互为相似三角形．
点评：本题考查了正方形的性质和相似三角形的判定定理，关键知道正方形的四边相等和熟记这些判定定理．
∵BP=3PC，
∴CP=
BC=CD，∵Q是CD的中点，
∴CQ=DQ=
AD．∴
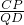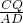==，又∵∠C=∠D．
∴△ADQ∽△QCP．
分析：正方形的四边相等，两个三角形的两组对应边成比例，夹角相等的两个三角形互为相似三角形．
点评：本题考查了正方形的性质和相似三角形的判定定理，关键知道正方形的四边相等和熟记这些判定定理．
练习册系列答案
状元坊全程突破导练测系列答案
直通贵州名校周测月考直通名校系列答案
相关题目
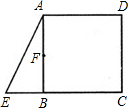已知：如图，在正方形ABCD中，E是CB延长线上一点，EB=
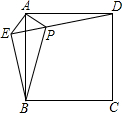已知：如图，在正方形ABCD外取一点E，连接AE、BE、DE．过点A作AE的垂线交DE于点P．若AE=AP=1，PB=
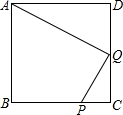已知：如图，在正方形ABCD中，P是BC上的点，且BP=3PC，Q是CD的中点．△ADQ与△QCP是否相似？
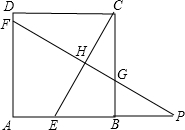、CE、CB于点F、H、G，交AB的延长线于点P．
已知：如图，在正方形ABCD中，E、F分别是AD、CD的中点．