题目内容
 如图,一次函数y=kx+b的图象与坐标轴分别交于点A(8,0)和B(0,6),再将△AOB沿直线CD折起,使点A与点B重合,直线CD与x轴交于点C,与AB交于点D.
如图,一次函数y=kx+b的图象与坐标轴分别交于点A(8,0)和B(0,6),再将△AOB沿直线CD折起,使点A与点B重合,直线CD与x轴交于点C,与AB交于点D.
(1)试确定直线AB的函数解析式;
(2)求点C的坐标.
(3)是否存在经过点E(2,0)的直线l将△OBA的面积分成1:3?如果存在求出直线的解析式,不存在试说明理由.
 解:(1)将A(8,0)与B(0,6)代入一次函数解析式得:
解:(1)将A(8,0)与B(0,6)代入一次函数解析式得: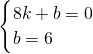 ,
,解得:
 ,
,则直线AB解析式为y=-
 x+6;
x+6;(2)连接BC,由折叠得到AC=BC,
∵A(8,0),B(0,6),
∴OA=8,OB=6,
在Rt△BOC中,设CB=CA=x,则有OC=OA-AC=8-x,
根据勾股定理得:BC2=OB2+OC2,即x2=(8-x)2+62,
解得:x=
 ,
,∴OC=8-x=
 ,即C(
,即C( ,0);
,0);(3)存在,做出直线EF,与直线AB交于点F,作FG⊥x轴,
根据题意得:S△AEF=
 S△ABC或S△AEF=
S△ABC或S△AEF= S△ABC,
S△ABC,即
 AE•FG=
AE•FG= ×
× OA•OB或
OA•OB或 AE•FG=
AE•FG= ×
× OA•OB,
OA•OB,由AE=OA-OE=8-2=6,OA=8,OB=6,
解得:FG=6或FG=2,
理由为:设过E的直线方程为y=a(x-2)=ax-2a,
与直线AB解析式联立消去y得:ax-2a=-
 x+6,
x+6,解得:x=
 ,
,∴y=a(
 -2)=6或2,
-2)=6或2,解得:a=-3或a=
 ,
,则满足题意的直线方程为y=-3x+6或y=
 x-
x- .
.分析:(1)将A与B坐标代入一次函数解析式求出k与b的值,即可确定出直线AB解析式;
(2)连接BC,由折叠的性质得到BC=AC,在直角三角形BOC中,设BC=AC=x,表示出OC=8-x,由OB=6,利用勾股定理列出关于x的方程,求出方程的解得到x的值,确定出OC的长,即可得出C坐标;
(3)存在,做出直线EF,与直线AB交于点F,作FG⊥x轴,根据题意得:S△AEF=
 S△ABC或S△AEF=
S△ABC或S△AEF= S△ABC,求出FG长,联立直线EF与AB,消去y表示出x,进而表示出y,根据纵坐标为EF列出关于a的方程,求出方程的解得到a的值,即可确定出满足题意的直线解析式.
S△ABC,求出FG长,联立直线EF与AB,消去y表示出x,进而表示出y,根据纵坐标为EF列出关于a的方程,求出方程的解得到a的值,即可确定出满足题意的直线解析式.点评:此题属于一次函数综合题,涉及的知识有:待定系数法求一次函数解析式,坐标与图形性质,勾股定理,利用了方程的思想,熟练掌握待定系数法是解本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 已知,如图,一次函数y1=-x-1与反比例函数y2=-
已知,如图,一次函数y1=-x-1与反比例函数y2=-| 2 |
| x |
| A、x>1 |
| B、x<-2或0<x<1 |
| C、-2<x<1 |
| D、-2<x<0或x>1 |
 如图,一次函数y=kx+2的图象与反比例函数y=
如图,一次函数y=kx+2的图象与反比例函数y= 13、如图,一次函数y=kx+b(k<0)的图象经过点A.当y<3时,x的取值范围是
13、如图,一次函数y=kx+b(k<0)的图象经过点A.当y<3时,x的取值范围是 (2013•成都)如图,一次函数y1=x+1的图象与反比例函数
(2013•成都)如图,一次函数y1=x+1的图象与反比例函数 如图,一次函数y=x+3的图象与x轴、y轴分别交于点A、点B,与反比例函数
如图,一次函数y=x+3的图象与x轴、y轴分别交于点A、点B,与反比例函数