题目内容
 如图所示,点P是反比例函数y=
如图所示,点P是反比例函数y=| k |
| x |
y=-
| 4 |
| x |
y=-
.| 4 |
| x |
分析:先根据反比例函数的图象在第二象限可知,k<0,再根据矩形面积是4可知|k|=4,故可得出k的值,进而得出结论.
解答:解:∵点P是反比例函数y=
图象上的一点,函数的图象在第二象限,
∴k<0,
∵矩形面积是4可知|k|=4,
∴k=-4,
∴反比例函数的解析式为:y=-
.
故答案为:y=-
.
| k |
| x |
∴k<0,
∵矩形面积是4可知|k|=4,
∴k=-4,
∴反比例函数的解析式为:y=-
| 4 |
| x |
故答案为:y=-
| 4 |
| x |
点评:本题考查的是反比例函数系数k的几何意义,即在反比例函数y=xk图象中任取一点,过这一个点向x轴和y轴分别作垂线,与坐标轴围成的矩形的面积是定值|k|.

练习册系列答案
相关题目
 反比例数
反比例数 的图象如图所示,点M是该函数图象上一点,MN垂直于x轴,垂足是点N,如果S△MON=2,则k的值为 .
的图象如图所示,点M是该函数图象上一点,MN垂直于x轴,垂足是点N,如果S△MON=2,则k的值为 .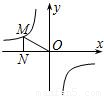
 的图象如图所示,点M是该函数图象上一点,MN垂直于x轴,垂足是点N,如果S△MON=2,则k的值为 .
的图象如图所示,点M是该函数图象上一点,MN垂直于x轴,垂足是点N,如果S△MON=2,则k的值为 .
 的图象如图所示,点M是该函数图象上一点,MN垂直于x轴,垂足是点N,如果S△MON=2,则k的值为 .
的图象如图所示,点M是该函数图象上一点,MN垂直于x轴,垂足是点N,如果S△MON=2,则k的值为 .
 的图象如图所示,点M是该函数图象上一点,MN垂直于x轴,垂足是点N,如果S△MON=2,则k的值为 .
的图象如图所示,点M是该函数图象上一点,MN垂直于x轴,垂足是点N,如果S△MON=2,则k的值为 .