题目内容
 如图所示,在等腰直角三角形ABC中,∠C=90°,点D在CB的延长线上,且BD=AB,求∠ADB的正切值.
如图所示,在等腰直角三角形ABC中,∠C=90°,点D在CB的延长线上,且BD=AB,求∠ADB的正切值.分析:由三角形ABC为等腰直角三角形,得到BC=AC,利用勾股定理表示出AB,将BC=AC代入,用AC表示出AB,再由BD=AB,表示出BD,由BC+BD表示出CD,所求角的正切值等于AC与CD的比值,求出即可.
解答: 解:在等腰直角三角形ABC中,BC=AC,
解:在等腰直角三角形ABC中,BC=AC,
根据勾股定理得:AB=
=
=
AC,
∵BD=AB=
AC,
∴CD=CB+BD=AC+
AC=(
+1)AC,
则tan∠ADB=
=
=
-1.
 解:在等腰直角三角形ABC中,BC=AC,
解:在等腰直角三角形ABC中,BC=AC,根据勾股定理得:AB=
| AC2+BC2 |
| AC2+AC2 |
| 2 |
∵BD=AB=
| 2 |
∴CD=CB+BD=AC+
| 2 |
| 2 |
则tan∠ADB=
| AC |
| CD |
| AC | ||
(
|
| 2 |
点评:此题属于解直角三角形题型,涉及的知识有:等腰直角三角形的性质,勾股定理,以及锐角三角函数定义,熟练运用勾股定理是解本题的关键.

练习册系列答案
 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案
相关题目
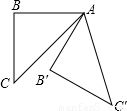
 4、如图所示,在等腰直角三角形ABC中,∠B=90°,将△ABC绕点A逆时针旋转60°后得到的△AB′C′,则∠BAC′等于( )
4、如图所示,在等腰直角三角形ABC中,∠B=90°,将△ABC绕点A逆时针旋转60°后得到的△AB′C′,则∠BAC′等于( )

 如图所示,在等腰直角三角形ABC中,∠C=90°,点D在CB的延长线上,且BD=AB,求∠ADB的正切值.
如图所示,在等腰直角三角形ABC中,∠C=90°,点D在CB的延长线上,且BD=AB,求∠ADB的正切值.