题目内容
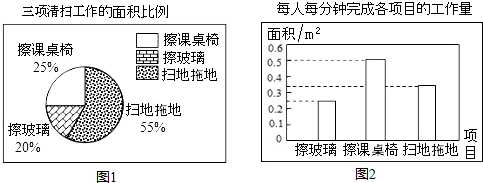
如图，在矩形ABCD中，点E是AB边上一点，连结CE，将矩形ABCD沿CE翻折得到△FCE，点F在矩形内部，连结AF．若AB=4，AF∥CE，则AE的长为考点：翻折变换（折叠问题）
专题：
分析：先证明EA=EF，再由折叠的性质可得AE=EF=EB，从而可求出AE．
解答：解：∵AF∥CE，
∴∠AFE=∠FEC，∠FAE=∠CEB，
由折叠的性质可得：∠FEC=∠CEB，
∴∠AFE=∠FAE，
∴EA=EF，
∴EA=EF=EB，
∴AE=
AB=2．
故答案为：2．
∴∠AFE=∠FEC，∠FAE=∠CEB，
由折叠的性质可得：∠FEC=∠CEB，
∴∠AFE=∠FAE，
∴EA=EF，
∴EA=EF=EB，
∴AE=
| 1 |
| 2 |
故答案为：2．
点评：本题考查了翻折变换，设计巧妙，由平行线的性质入手，证明EA=EF是解题关键．
练习册系列答案
芒果教辅达标测试卷系列答案
相关题目
如图，直线a、b被直线c所截，若满足
一个几何体的三视图如图，根据图示的数据计算该几何体的全面积为不等式组
的解集是（ ）
|
| A、x＞-1 | B、x＞2 |
| C、-1＜x＜2 | D、x＜2 |
