ЬтФПФкШн
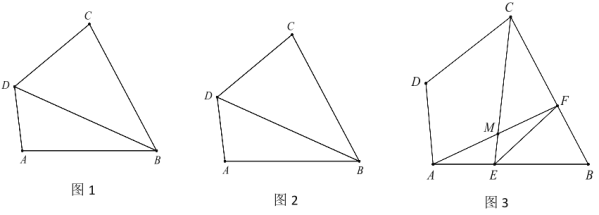
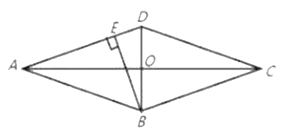
ЁОЬтФПЁПвбжЊЃКЁбOЪЧЁїABCЕФЭтНгдВЃЌЕуMЮЊЁбOЩЯвЛЕу.
ЃЈ1ЃЉШчЭМЃЌШєЁїABCЮЊЕШБпШ§НЧаЮЃЌBM=1ЃЌCM=2ЃЌЧѓAMЕФГЄЃЛ

аЁУїдкНтОіетИіЮЪЬтЪБВЩгУЕФЗНЗЈЪЧЃКбгГЄMCЕНEЃЌЪЙME=AMЃЌДгЖјПЩжЄЁїAMEЮЊЕШБпШ§НЧаЮЃЌВЂЧвЁїABMЁеЁїACEЃЌНјЖјОЭПЩЧѓГіЯпЖЮAMЕФГЄЃЎ
ЧыФуНшМјаЁУїЕФЗНЗЈаДГіAMЕФГЄЃЌВЂаДГіЭЦРэЙ§ГЬЃЎ
ЃЈ2ЃЉШєЁїABCЮЊЕШбќжБНЧШ§НЧаЮЃЌЁЯBAC=90ЁуЃЌ![]() ЃЌЃЈЦфжаbЃОaЃЉЃЌжБНгаДГіAMЕФГЄ(гУКЌгаaЃЌbЕФДњЪ§ЪНБэЪО).
ЃЌЃЈЦфжаbЃОaЃЉЃЌжБНгаДГіAMЕФГЄ(гУКЌгаaЃЌbЕФДњЪ§ЪНБэЪО).
ЁОД№АИЁПAMЕФГЄЪЧ![]() (a+b)Лђ
(a+b)Лђ![]() (b-a)ЃЎ
(b-a)ЃЎ
ЁОНтЮіЁП
ЪдЬтЃЈ1ЃЉбгГЄMBжСЕуEЃЌЪЙBE=MCЃЌСЌAEЃЌИљОнЕШБпШ§НЧаЮаджЪЧѓГіAC=ABЃЌИљОндВФкНгЫФБпаЮЕФаджЪЭЦГіЁЯABE=ЁЯACMЃЌжЄЁїABEЁеЁїACMЃЌЭЦГіAM=AEЃЌжЄЕШБпШ§НЧAEMЃЌЭЦГіAE=AM=MEЃЌМДПЩЭЦГіД№АИЃЛ
ЃЈ2ЃЉЗжЮЊСНжжЧщПіЃЌЛГіЭМаЮЃЌбгГЄMBжСЕуEЃЌЪЙBE=MCЃЌСЌAEЃЌИљОнЕШбќжБНЧШ§НЧаЮаджЪЭЦГіAB=ACЃЌИљОнSASжЄЁїABEЁеЁїACMЃЌЭЦГіAM=AEЃЌЁЯE=ЁЯAMC=45ЁуЃЌЁЯAMB=45ЁуЃЌЧѓГіЁїEAMЪЧЕШбќжБНЧШ§НЧаЮЃЌИљОнЙДЙЩЖЈРэЧѓГіМДПЩЃЎ
ЃЈ1ЃЉНтЃКбгГЄMBжСЕуEЃЌЪЙBE=MCЃЌСЌНгAEЃЌ
ЁпЁїABCЪЧЕШБпШ§НЧаЮЃЌ
ЁрAB=ACЃЌ
ЁпЫФБпаЮABMCЪЧЁбOЕФФкНгЫФБпаЮЃЌ
ЁрЁЯABE=ЁЯACMЃЌ

дкЁїAEBКЭЁїAMCжаЃЌ ЁрЁїAEBЁеЁїAMCЃЌ
ЁрЁїAEBЁеЁїAMCЃЌ
ЁрЁЯAEB=ЁЯAMCЃЌ
ЁпЁЯAMC=ЁЯABCЃЈдкЭЌдВжаЃЌЭЌЛЁЫљЖдЕФдВжмНЧЯрЕШЃЉЃЌ
ЁрЁЯAEB=ЁЯABCЃЌ
ЁпЁЯAME=ЁЯACBЃЈдкЭЌдВжаЃЌЭЌЛЁЫљЖдЕФдВжмНЧЯрЕШЃЉЃЌ
гжЁпЁЯABC=ЁЯACB=60ЁуЃЌ
ЁрЁЯAEB=ЁЯAME=60ЁуЃЌ
ЁрЁїAEMЪЧЕШБпШ§НЧаЮЃЌ
ЁрAM=ME=MB+BEЃЌ
ЁпBE=MCЃЌ
ЁрMB+MC=MA=1+2=3ЃЎ
МДAMЕФГЄЪЧ3ЃЎ
ЃЈ2ЃЉНтЃКЗжЮЊСНжжЧщПіЃКЂйШчЭМЃЌ

бгГЄMBжСЕуEЃЌЪЙBE=MCЃЌСЌAEЃЌ
гЩЃЈ1ЃЉжЊЃКЁЯABE=ЁЯACMЃЌ
дкЁїABEКЭЁїACMжа
ЁрЁїABEЁеЁїACMЃЌ
ЁрAM=AEЃЌЁЯE=ЁЯAMCЃЌ
ЁпЁЯAMC=ЁЯABC=45ЁуЃЌЁЯAMB=ЁЯACB=45ЁуЃЌ
ЁрЁЯE=ЁЯAMB=45ЁуЃЌ
ЁрЁЯEAM=90ЁуЃЌ
дкЁїEAMжаЃЌME=MB+BE=MB+CM=a+bЃЌAE=AMЃЌ
гЩЙДЙЩЖЈРэЕУЃКAM=![]() (a+b)
(a+b)
МДAM=![]() (a+b)
(a+b)
ЂкШчЭМЃЌ

дкCMЩЯНиШЁCN=BMЃЌСЌНгANЃЌ
ЁпЁЯABMЫљЖдЕФЛЁКЭЁЯACNЫљЖдЕФЛЁЖМЪЧЛЁAMЃЌ
ЁрЁЯABM=ЁЯACNЃЌ
дкЁїABMКЭЁїACNжа
ЁрЁїABMЁеЁїACNЃЈSASЃЉЃЌ
ЁрAM=ANЃЌЁЯBAM=ЁЯCANЃЌ
ЁпЁЯBAC=ЁЯBAN+ЁЯCAN=90ЁуЃЌ
ЁрЁЯBAN+ЁЯBAM=90ЁуЃЌ
ЁрЁЯMAN=90ЁуЃЌ
дђЁїMANЪЧЕШбќжБНЧШ§НЧаЮЃЌ
ЁпMN=CM-CN=CM-BM=b-aЃЌ
гЩЙДЙЩЖЈРэЕУЃКAM=AN=![]() (b-a)
(b-a)
МДAM=![]() (b-a)ЃЎ
(b-a)ЃЎ
МДAMЕФГЄЪЧ![]() (a+b)Лђ
(a+b)Лђ![]() (b-a)ЃЎ
(b-a)ЃЎ

 гХЕШЩњЬтПтЯЕСаД№АИ
гХЕШЩњЬтПтЯЕСаД№АИ