题目内容
如图1,M是边长为4的正方形AD边的中点,动点P自A点起,由A?B?C?D匀速运动,直线MP扫过正方形所形成的面积为Y,点P运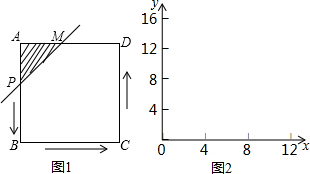 动的路程为X,请解答下列问题:
动的路程为X,请解答下列问题:
(1)当x=1时,求y的值;
(2)就下列各种情况,求y与x之间的函数关系式:
①0≤x≤4;②4<x≤8 ③8<x≤12;
(3)在给出的直角坐标系(图2)中,画出(2)中函数的图象.
解:(1)由题意,x=1时,AP=1,
∴y= AM•AP=
AM•AP= ×2×1=1;
×2×1=1;
(2)①当0≤x≤4时,点P由A→B在AB线段上运动,AP=x,
直线MP扫过正方形所形成的图形为Rt△MAP,
其面积为:y1= AM•AP=
AM•AP= ×2×x=x;
×2×x=x;
②当4<x≤8时,点P由B→C在BC线段上运动,BP=x-4,直线MP扫过正方形所形成的图形为梯形MABP,
其面积为:y2= (AM+BP)•AB=
(AM+BP)•AB= [2+(x-4)]×4=2x-4;
[2+(x-4)]×4=2x-4;
③当8<x≤12时,点P由C→D在CD线段上运动,DP=12-x.直线MP扫过正方形所形成的图形为五边形MABCP,
其面积为:y3=S正方形ABCD-SRt△MPD=42- MD•DP=16-
MD•DP=16- ×2×(12-x)=x+4;
×2×(12-x)=x+4;
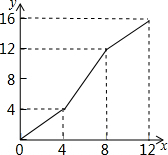
(3)
 .
.
分析:(1)直接根据三角形的面积公式可得y= AM•AP=1;
AM•AP=1;
(2)①当0≤x≤4时,AP=x,直线MP扫过正方形所形成的图形为Rt△MAP,其面积为:y1= AM•AP=
AM•AP= ×2×x=x;
×2×x=x;
②当4<x≤8时,BP=x-4,直线MP扫过正方形所形成的图形为梯形MABP,其面积为:y2= (AM+PB)•AB=
(AM+PB)•AB= [2+(x-4)]×4=2x-4;
[2+(x-4)]×4=2x-4;
③当8<x≤12时,DP=12-x.直线MP扫过正方形所形成的图形为五边形MABCP,其面积为:y3=S正方形ABCD-SRt△MPD=x+4;
(3)分别描出点(4,4),(8,12),(12,16),连线即可.
点评:主要考查了函数和几何图形的综合运用.解题的关键是会灵活的运用函数图象的性质和交点的意义求出相应的线段的长度或表示线段的长度,再结合具体图形的性质求解.
∴y=
 AM•AP=
AM•AP= ×2×1=1;
×2×1=1;(2)①当0≤x≤4时,点P由A→B在AB线段上运动,AP=x,
直线MP扫过正方形所形成的图形为Rt△MAP,
其面积为:y1=
 AM•AP=
AM•AP= ×2×x=x;
×2×x=x;②当4<x≤8时,点P由B→C在BC线段上运动,BP=x-4,直线MP扫过正方形所形成的图形为梯形MABP,
其面积为:y2=
 (AM+BP)•AB=
(AM+BP)•AB= [2+(x-4)]×4=2x-4;
[2+(x-4)]×4=2x-4;③当8<x≤12时,点P由C→D在CD线段上运动,DP=12-x.直线MP扫过正方形所形成的图形为五边形MABCP,
其面积为:y3=S正方形ABCD-SRt△MPD=42-
 MD•DP=16-
MD•DP=16- ×2×(12-x)=x+4;
×2×(12-x)=x+4;(3)
 .
.分析:(1)直接根据三角形的面积公式可得y=
 AM•AP=1;
AM•AP=1;(2)①当0≤x≤4时,AP=x,直线MP扫过正方形所形成的图形为Rt△MAP,其面积为:y1=
 AM•AP=
AM•AP= ×2×x=x;
×2×x=x;②当4<x≤8时,BP=x-4,直线MP扫过正方形所形成的图形为梯形MABP,其面积为:y2=
 (AM+PB)•AB=
(AM+PB)•AB= [2+(x-4)]×4=2x-4;
[2+(x-4)]×4=2x-4;③当8<x≤12时,DP=12-x.直线MP扫过正方形所形成的图形为五边形MABCP,其面积为:y3=S正方形ABCD-SRt△MPD=x+4;
(3)分别描出点(4,4),(8,12),(12,16),连线即可.
点评:主要考查了函数和几何图形的综合运用.解题的关键是会灵活的运用函数图象的性质和交点的意义求出相应的线段的长度或表示线段的长度,再结合具体图形的性质求解.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 动的路程为X,请解答下列问题:
动的路程为X,请解答下列问题: (2012•营口)如图,四边形ABCD是边长为60cm的正方形硬纸片,剪掉阴影部分所示的四个全等的等腰直角三角形,再沿虚线折起,使A、B、C、D四个点重合于图中的点P,正好形成一个底面是正方形的长方体包装盒.
(2012•营口)如图,四边形ABCD是边长为60cm的正方形硬纸片,剪掉阴影部分所示的四个全等的等腰直角三角形,再沿虚线折起,使A、B、C、D四个点重合于图中的点P,正好形成一个底面是正方形的长方体包装盒.
 如图,四边形ABCD是边长为9的正方形纸片,沿MN折叠,使点B落在CD边上的B′处,点A对应点A′,且B′C=3,求CN和AM的长.
如图,四边形ABCD是边长为9的正方形纸片,沿MN折叠,使点B落在CD边上的B′处,点A对应点A′,且B′C=3,求CN和AM的长. 如图,四边形ABCD是边长为1的正方形,点F在BC延长线上,且CF=AC,AF与DC交于点E.求:
如图,四边形ABCD是边长为1的正方形,点F在BC延长线上,且CF=AC,AF与DC交于点E.求: