题目内容
 如图,在△ABC中,∠ACB=90°,AC=BC,BE⊥CE于E,AD⊥CE于D,AD=5cm,DE=3cm,你知道BE的长吗?
如图,在△ABC中,∠ACB=90°,AC=BC,BE⊥CE于E,AD⊥CE于D,AD=5cm,DE=3cm,你知道BE的长吗?考点:全等三角形的判定与性质
专题:
分析:易证△ACD≌△CBE,即可求得AD=CE,BE=CD,即可解题.
解答:解:∵∠BCE+∠ACD=90°,∠ACD+∠DAC=90°,
∴∠BCE=∠DAC,
∵在△BCE和△ACD中,
,
∴△BCE≌△ACD,(AAS)
∴AD=CE,BE=CD
∴BE=CD=CE-DE=AD-DE=2cm.
∴∠BCE=∠DAC,
∵在△BCE和△ACD中,
|
∴△BCE≌△ACD,(AAS)
∴AD=CE,BE=CD
∴BE=CD=CE-DE=AD-DE=2cm.
点评:本题考查了全等三角形的判定和全等三角形对应边相等的性质,本题中求证△BCE≌△ACD是解题的关键.

练习册系列答案
相关题目
代数式(
)2与代数式(
)2的差是( )
| x+y |
| 2 |
| x-y |
| 2 |
| A、xy | ||
| B、2xy | ||
C、
| ||
| D、0 |
 在如图的三角形中,用三角尺或量角器过点A作BC的垂线,过点B作AC的垂线,过点C作AB的垂线.
在如图的三角形中,用三角尺或量角器过点A作BC的垂线,过点B作AC的垂线,过点C作AB的垂线. ABCD为一矩形纸片,AB=
ABCD为一矩形纸片,AB=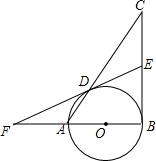 如图,在△ABC中,∠ABC=90°,AB=4,BC=5,以AB为直径的⊙O交AC于点D,点E是BC的中点,连接ED并延长交BA的延长线于点F.
如图,在△ABC中,∠ABC=90°,AB=4,BC=5,以AB为直径的⊙O交AC于点D,点E是BC的中点,连接ED并延长交BA的延长线于点F.