题目内容
 若实数a,b,c在数轴上的位置如图,
若实数a,b,c在数轴上的位置如图,化简:(1)
| a2 |
| c2 |
| (a-c)2 |
(2)|a-b|-|c-a|+|b-c|-
| a2 |
分析:首先观察数轴,可得a<b<0<c,
(1)由二次根式的性质,即可将原式化简为:-a-c+(-a+c),然后去括号,合并同类项,即可求得答案;
(2)首先去绝对值,化简二次根式,即可将原式化简为:b-a-(c-a)+(c-b)-(-a)然后去括号,合并同类项,即可求得答案.
(1)由二次根式的性质,即可将原式化简为:-a-c+(-a+c),然后去括号,合并同类项,即可求得答案;
(2)首先去绝对值,化简二次根式,即可将原式化简为:b-a-(c-a)+(c-b)-(-a)然后去括号,合并同类项,即可求得答案.
解答:解:如图,可得:a<b<0<c,
(1)原式=|a|-|c|+|a-c|
=-a-c+(-a+c)
=-a-c-a+c
=-2a;
(2)原式=b-a-(c-a)+(c-b)-(-a)
=b-a-c+a+c-b+a
=a.
(1)原式=|a|-|c|+|a-c|
=-a-c+(-a+c)
=-a-c-a+c
=-2a;
(2)原式=b-a-(c-a)+(c-b)-(-a)
=b-a-c+a+c-b+a
=a.
点评:此题考查了二次根式的性质与化简,以及绝对值的性质.此题难度适中,注意掌握二次根式与绝对值的性质是解此题的关键.

练习册系列答案
相关题目

 .该方法在数、式、方程等多方面应用非常广泛,如
.该方法在数、式、方程等多方面应用非常广泛,如

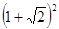 ;
;
 =
= 等等.请你用配方法解决以下问题:
等等.请你用配方法解决以下问题: ;(不能出现形如
;(不能出现形如 的双重二次根式)
的双重二次根式) ,解关于x的一元二次方程
,解关于x的一元二次方程 ;
; 总有两个不等实数根
总有两个不等实数根