题目内容
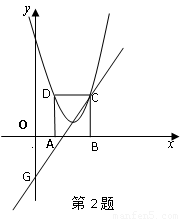
 如图,E、F分别是矩形ABCD的边AB、BC的中点,连CE、AF,设CE、AF相交于G,则S四边形BEGF:S四边形ABCD等于
如图,E、F分别是矩形ABCD的边AB、BC的中点,连CE、AF,设CE、AF相交于G,则S四边形BEGF:S四边形ABCD等于
- A.

- B.

- C.

- D.

C
分析:可过点G作AB、BC的垂线,连接BG,将四边形GEBF分为△BEG与△BGF两部分,得出四边形GEBF与△GFC的关系,进而再通过转化即可得出结论.
解答: 解:如图,
解:如图,
过点G作AB、BC的垂线,连接BG,AC,
S矩形ABCD=AB•BC,
S△BCE= •
• AB•BC,S△ABF=
AB•BC,S△ABF= •AB•
•AB• BC,
BC,
S△AEG=S△GCF,即AE•GN=CF•GM,
SGEBF=S△BEG+S△BFG= BE•GN+
BE•GN+ BF•GM=2S△AEG=2S△GCF,
BF•GM=2S△AEG=2S△GCF,
∴S△BCE=3S△GCF= AB•BC,
AB•BC,
∴SGEBF=2S△GCF= AB•AC.
AB•AC.
故选C.
点评:本题主要考查了矩形的性质以及三角形面积的计算问题,应熟练掌握.
分析:可过点G作AB、BC的垂线,连接BG,将四边形GEBF分为△BEG与△BGF两部分,得出四边形GEBF与△GFC的关系,进而再通过转化即可得出结论.
解答:
 解:如图,
解:如图,过点G作AB、BC的垂线,连接BG,AC,
S矩形ABCD=AB•BC,
S△BCE=
 •
• AB•BC,S△ABF=
AB•BC,S△ABF= •AB•
•AB• BC,
BC,S△AEG=S△GCF,即AE•GN=CF•GM,
SGEBF=S△BEG+S△BFG=
 BE•GN+
BE•GN+ BF•GM=2S△AEG=2S△GCF,
BF•GM=2S△AEG=2S△GCF,∴S△BCE=3S△GCF=
 AB•BC,
AB•BC,∴SGEBF=2S△GCF=
 AB•AC.
AB•AC.故选C.
点评:本题主要考查了矩形的性质以及三角形面积的计算问题,应熟练掌握.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案
相关题目

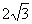 ,直线y=
,直线y=
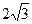 ,直线y=
,直线y=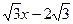 经过点C,交y轴于点G
经过点C,交y轴于点G
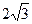 ,直线y=
,直线y=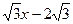 经过点C,交y轴于点G
经过点C,交y轴于点G
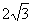 ,直线y=
,直线y=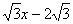 经过点C,交y轴于点G
经过点C,交y轴于点G