题目内容
 如图,直线l1、l2相交于点O,点P关于l1、l2的对称点分别为P1、P2.
如图,直线l1、l2相交于点O,点P关于l1、l2的对称点分别为P1、P2.
(1)若l1、l2相交所成的锐角∠AOB=65°,则∠P1OP2=______°;
(2)若OP=4,P1P2=7,则△P1OP2的周长为______.
解:(1)∵P关于l1、l2的对称点分别为P1、P2,
∴∠P1AO=∠AOP,∠P2OB=∠POB,
∴∠P1OP2=2(∠AOP+∠POB)=2∠AOB=2×65°=130°;
(2)∵P关于l1、l2的对称点分别为P1、P2,
∴OP1=OP=OP2=4,
∵P1P2=7,
∴△P1OP2的周长=OP1+OP2+P1P2=4+4+7=15.
故答案为:130°、15.
分析:(1)由于P关于l1、l2的对称点分别为P1、P2,可得出∠P1AO=∠AOP,∠P2OB=∠POB,再根据∠AOB=65°即可求解;
(2)根据对称的性质可知,OP1=OP=OP2=4,再根据P1P2=7即可求出△P1OP2的周长.
点评:本题考查的是最短路线问题及轴对称的性质,熟知轴对称的性质是解答此题的关键.
∴∠P1AO=∠AOP,∠P2OB=∠POB,
∴∠P1OP2=2(∠AOP+∠POB)=2∠AOB=2×65°=130°;
(2)∵P关于l1、l2的对称点分别为P1、P2,
∴OP1=OP=OP2=4,
∵P1P2=7,
∴△P1OP2的周长=OP1+OP2+P1P2=4+4+7=15.
故答案为:130°、15.
分析:(1)由于P关于l1、l2的对称点分别为P1、P2,可得出∠P1AO=∠AOP,∠P2OB=∠POB,再根据∠AOB=65°即可求解;
(2)根据对称的性质可知,OP1=OP=OP2=4,再根据P1P2=7即可求出△P1OP2的周长.
点评:本题考查的是最短路线问题及轴对称的性质,熟知轴对称的性质是解答此题的关键.

练习册系列答案
 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案
相关题目
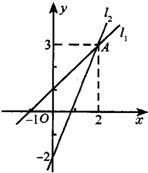 -2),结合图象解答下列问题:
-2),结合图象解答下列问题: 4、如图,直线l1,l2,l3相交于一点,则下列答案中,全对的一组是( )
4、如图,直线l1,l2,l3相交于一点,则下列答案中,全对的一组是( ) 如图,直线l1与l2相交于点O,OM⊥l1,若∠α=44°,则∠β等于
如图,直线l1与l2相交于点O,OM⊥l1,若∠α=44°,则∠β等于 如图,直线l1、l2、l3分别过正方形ABCD的三个顶点A,B,D,且相互平行,若l1与l2的距离为1,l2与l3的距离为1,则该正方形的面积是
如图,直线l1、l2、l3分别过正方形ABCD的三个顶点A,B,D,且相互平行,若l1与l2的距离为1,l2与l3的距离为1,则该正方形的面积是 如图,直线l1与l2相交于点P,l1的函数表达式y=kx+b,且经过(1,7)和(-3,-1)两点,点P的横坐标为-1,且l2交y轴于点A(0,-1).
如图,直线l1与l2相交于点P,l1的函数表达式y=kx+b,且经过(1,7)和(-3,-1)两点,点P的横坐标为-1,且l2交y轴于点A(0,-1).