题目内容
(初三)关于x的方程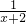 -
- =1-
=1- 有两个实根,则k应满足
有两个实根,则k应满足
- A.k2-18k+33>0
- B.k2-18k+33>0且k≠-2
- C.k2-18k+33>0且k≠2
- D.k2-18k+33>0且k≠±2
A
分析:观察可得最简公分母是(x+2)(x-2),方程两边乘最简公分母,可以把分式方程转化为整式方程求解.
解答:方程两边同乘以(x+2)(x-2),
得x-2-k(x+2)=(x+2)(x-2)-4x,
化简得
x2+(k-5)x+(2k-2)=0,
又∵方程有两个实根,
∴△=b2-4ac=(k-5)2-4×1×(2k-2)=k2-18k+33>0,
故选A.
点评:本题考查了解分式方程、根的判别式.
(1)解分式方程的基本思想是“转化思想”,把分式方程转化为整式方程求解.
(2)解分式方程一定注意要验根.
分析:观察可得最简公分母是(x+2)(x-2),方程两边乘最简公分母,可以把分式方程转化为整式方程求解.
解答:方程两边同乘以(x+2)(x-2),
得x-2-k(x+2)=(x+2)(x-2)-4x,
化简得
x2+(k-5)x+(2k-2)=0,
又∵方程有两个实根,
∴△=b2-4ac=(k-5)2-4×1×(2k-2)=k2-18k+33>0,
故选A.
点评:本题考查了解分式方程、根的判别式.
(1)解分式方程的基本思想是“转化思想”,把分式方程转化为整式方程求解.
(2)解分式方程一定注意要验根.

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
(初三)关于x的方程
-
=1-
有两个实根,则k应满足( )
| 1 |
| x+2 |
| k |
| x-2 |
| 4x |
| x2-4 |
| A、k2-18k+33>0 |
| B、k2-18k+33>0且k≠-2 |
| C、k2-18k+33>0且k≠2 |
| D、k2-18k+33>0且k≠±2 |