题目内容
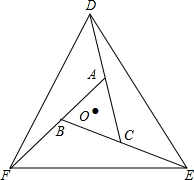 如图所示,已知△ABC的三个外角都是120°,点D、E、F分别是CA、BC、AB延长线上的一点,且AD=AC,CE=CB,AB=BF,连接ED、EF、FD,
如图所示,已知△ABC的三个外角都是120°,点D、E、F分别是CA、BC、AB延长线上的一点,且AD=AC,CE=CB,AB=BF,连接ED、EF、FD,(1)试判断△DEF是什么三角形?
(2)若点O是△ABC三条中线的交点,以点O为旋转中心,则△DEF旋转多少度后能与原来的图形重合?
考点:旋转的性质
专题:常规题型
分析:(1)由于△ABC的三个外角都是120°,则△ABC的三个内角都是60°,所以可判断△ABC为等边三角形,则AB=AC=BC,再利用AD=AC,CE=CB,AB=BF得到AF=BE=CD,AD=BF=CE,则根据“SAS”可证明△ADF≌△CDE,得到DF=DE,同理可得DF=FE,即DF=DE=FE,于是可判断△DEF为等边三角形;
(2)由于点O是等边△ABC三条中线的交点,根据等边三角形的性质得点O为△ABC的中心,加上△DEF为等边三角形,得到点O为△DEF的中心,然后根据等边三角形的中心角为120度得到以点O为旋转中心,△DEF旋转120度后能与原来的图形重合.
(2)由于点O是等边△ABC三条中线的交点,根据等边三角形的性质得点O为△ABC的中心,加上△DEF为等边三角形,得到点O为△DEF的中心,然后根据等边三角形的中心角为120度得到以点O为旋转中心,△DEF旋转120度后能与原来的图形重合.
解答:解:(1)△DEF为等边三角形.理由如下:
∵△ABC的三个外角都是120°,
∴△ABC的三个内角都是60°,
∴△ABC为等边三角形,
∴AB=AC=BC,
∵AD=AC,CE=CB,AB=BF,
∴AF=BE=CD,AD=BF=CE,
在△ADF和△CDE中,
,
∴△ADF≌△CDE(SAS),
∴DF=DE,
同理可得△ADF≌△BFE,
∴DF=FE,
∴DF=DE=FE,
∴△DEF为等边三角形;
(2)∵点O是等边△ABC三条中线的交点,即点O为△ABC的中心,
而△DEF为等边三角形,
∴点O为△DEF的中心,
∴以点O为旋转中心,△DEF旋转120度后能与原来的图形重合.
∵△ABC的三个外角都是120°,
∴△ABC的三个内角都是60°,
∴△ABC为等边三角形,
∴AB=AC=BC,
∵AD=AC,CE=CB,AB=BF,
∴AF=BE=CD,AD=BF=CE,
在△ADF和△CDE中,
|
∴△ADF≌△CDE(SAS),
∴DF=DE,
同理可得△ADF≌△BFE,
∴DF=FE,
∴DF=DE=FE,
∴△DEF为等边三角形;
(2)∵点O是等边△ABC三条中线的交点,即点O为△ABC的中心,
而△DEF为等边三角形,
∴点O为△DEF的中心,
∴以点O为旋转中心,△DEF旋转120度后能与原来的图形重合.
点评:本题考查了旋转的性质:对应点到旋转中心的距离相等;对应点与旋转中心所连线段的夹角等于旋转角;旋转前、后的图形全等.也考查了等边三角形的判定与性质.

练习册系列答案
 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案
相关题目
下列说法中正确的是( )
A、
| ||
B、
| ||
| C、2+a是单项式 | ||
| D、πr2是多项式 |
小明说
为方程ax+by=10的解,小惠说
为方程ax+by=10的解.两人谁也不能说服对方,如果你想让他们的解都正确,则需要添加的条件是( )
|
|
| A、a=12,b=10 |
| B、a=9,b=10 |
| C、a=10,b=11 |
| D、a=10,b=10 |
下列算式中,正确的是( )
A、(24×
| ||||||||
B、-3.5÷
| ||||||||
C、(-6)÷(-4)÷(1
| ||||||||
D、-
|
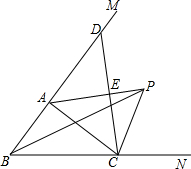 如图:△ABC中,∠ABC的平分线与∠ACB的外角的平分线相交于点P,连接AP.
如图:△ABC中,∠ABC的平分线与∠ACB的外角的平分线相交于点P,连接AP.