题目内容
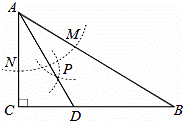
如图,在矩形ABCD中,AB=4,BC=3,将矩形绕点C按顺时针方向旋转,使点B落在线段AC上,得矩形CEFG,边CD与EF交于点H,连接DG.
(1)CH= .
(2)求DG的长.

解:(1)在矩形ABCD中,∵AB=4,BC=3,
∴AC= =
= =5,
=5,
∵矩形ABCD绕点C按顺时针方向旋转得矩形CEFG,
∴CE=BC=3,
∵∠BAC+∠ACB=90°,∠ECH+∠ACB=90°,
∴∠BAC=∠ECH,
又∵∠B=∠CEH=90°,
∴△ABC∽△CEH,
∴ =
= ,
,
即 =
= ,
,
解得CH= ;
;
故答案为: ;
;
(2)如图,过点G作GM⊥CD于M,
∵∠ACB+∠ACD=∠GCM+∠ACD=90°,
∴∠ACB=∠GCM,
又∵∠B=∠GMC=90°,
∴△ABC∽△GMC,
∴ =
= =
= ,
,
即 =
= =
= ,
,
解得CM= ,MG=
,MG= ,
,
∴DM=CD﹣CM=4﹣ =
= ,
,
在Rt△DMG中,DG= =
= =
= .
.


练习册系列答案
 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目

 B.
B. C.
C.
 D.
D. 

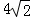 ,求点G到BE的距离.
,求点G到BE的距离.
 CD长为半径画弧,两弧交于点P,作射线OP.由作法得△OCP≌△ODP的根据是( )
CD长为半径画弧,两弧交于点P,作射线OP.由作法得△OCP≌△ODP的根据是( )
 点M和N,再分别以M、N为圆心,大于MN的长为半径画弧,两弧交于点P,连结AP并延长交BC于点D,则下列说法中正确的个数是( )
点M和N,再分别以M、N为圆心,大于MN的长为半径画弧,两弧交于点P,连结AP并延长交BC于点D,则下列说法中正确的个数是( )