题目内容
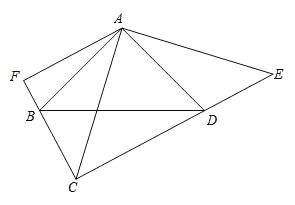
【题目】如图，矩形ABCD的对角线交于点O，点E是矩形外一点，
，
，
，连接AE交BD于点F、连接CF．
求证：四边形BECO是菱形；
填空：若
，则线段CF的长为______．
【答案】（1）详见解析；（2）
【解析】
（1）根据平行四边形的判定定理得到四边形OBEC是平行四边形，根据矩形的性质得到AC＝BD，OB＝
BD，OC＝AC，根据菱形的判定定理即可得到结论；
（2）根据平行线的性质得到∠OAF＝∠BEF，根据全等三角形的性质得到OF＝BF，推出△OBC是等边三角形，根据等边三角形的性质得到CF⊥OB，解直角三角形即可得到结论．
解：
，
，
四边形OBEC是平行四边形，
四边形ABCD是矩形，
，
，
，
，
平行四边形OBEC是菱形；
，
，
，
在
与
中，
，
≌
，
，
，
，
，
，
，
是等边三角形，
，
．
故答案为：．
练习册系列答案
相关题目
