题目内容
18.某校招聘学生会干部一名.对A.B.C三名候选人进行了四项素质测试,他们的各项测试成绩如下表所示:| 测试项目 | 测试成绩/分 | |||
| A | B | C | ||
| 语言 | 85 | 95 | 90 | |
| 综合知识 | 90 | 85 | 95 | |
| 创新 | 95 | 95 | 80 | |
| 处理问题能力 | 95 | 90 | 95 | |
分析 分别计算甲、乙、丙三人的加权平均数,然后比较平均数的大小,平均数大的将被录用.
解答 解:A的平均数=$\frac{2}{10}$×85+$\frac{3}{10}$×90+$\frac{3}{10}$×95+$\frac{2}{10}$×95=91.5,
B的平均数=$\frac{2}{10}$×95+$\frac{3}{10}$×85+$\frac{3}{10}$×95+$\frac{2}{10}$×90=91,
C的平均数=$\frac{2}{10}$×90+$\frac{3}{10}$×95+$\frac{3}{10}$×80+$\frac{2}{10}$×95=89.5
所以甲的成绩最高,
所以甲将被录用.
点评 本题考查了加权平均数:若n个数x1,x2,x3,…,xk的权分别是w1,w2,w3,…,wK,则$\frac{1}{n}$(x1w1+x2w2+…+xkwk)叫做这n个数的加权平均数.权的表现形式,一种是比的形式,如4:3:2,另一种是百分比的形式,如创新占50%,综合知识占30%,语言占20%,权的大小直接影响结果.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
9.在三角形的三个内角中:①最少有两个锐角;②最多有一个直角;③最多有一个钝角.上述说法正确的有( )
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
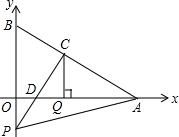 如图,在平面直角坐标系中,点A、B的坐标分别为(6,0),(0,3),动点P从原点O出发沿y轴负半轴方向以每秒1个单位的速度运动,同时动点Q从点O出发沿射线OA方向以每秒2个单位的速度运动,过点Q作CQ⊥x轴交直线AB于点C,连接AP,CP,CP交x轴于点D,设点P运动的时间为t秒.
如图,在平面直角坐标系中,点A、B的坐标分别为(6,0),(0,3),动点P从原点O出发沿y轴负半轴方向以每秒1个单位的速度运动,同时动点Q从点O出发沿射线OA方向以每秒2个单位的速度运动,过点Q作CQ⊥x轴交直线AB于点C,连接AP,CP,CP交x轴于点D,设点P运动的时间为t秒.