题目内容
已知抛物线的函数解析式为y＝ax2＋bx－3a（b＜0），若这条抛物线经过点（0，－3），方程ax2＋bx－3a＝0的两根为x1，x2，且|x1－x2|＝4．
⑴求抛物线的顶点坐标．
⑵已知实数x＞0，请证明x＋
≥2，并说明x为何值时才会有x＋＝2．
解：（1）∵抛物线过（0，－3）点，∴－3a＝－3 ∴a＝1 ∴y＝x2＋bx－3
∵x2＋bx－3＝0的两根为x1，x2， ∴
,
·
=-3
∵
＝4∴
＝4
∴
∴
∵b＜0 ∴b＝－2
∴y＝x2－2x－3＝（x－1）２－4 ∴抛物线的顶点坐标为（1，－4）
（2）∵x＞0，∴
∴
显然当x＝1时，才有
练习册系列答案
名校练考卷期末冲刺卷系列答案
相关题目
的函数解析式为
，若抛物线
，请证明：
≥
,并说明
为何值时才会有
.
，设
用含有
的表达式表示出△
的面积
，并求出
的函数解析式。
，则
，
两点间的距离为）
≥2，并说明x为何值时才会有x＋
≥2，并说明x为何值时才会有x+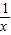
=2．
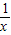≥2，并说明x为何值时才会有x＋