题目内容
已知p2-2p-5=0,5q2+2q-1=0,其中p、q为实数,求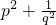 的值.
的值.
解:(1)当p≠ 时,p、
时,p、 是关于x的方程x2-2x-5=0的两个不相等的实数根,
是关于x的方程x2-2x-5=0的两个不相等的实数根,
则p+ =2,p•
=2,p• =-5,
=-5,
所以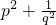 =
=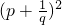 -2p•
-2p• =4-2×(-5)=14;
=4-2×(-5)=14;
(2)当p= 时,p、
时,p、 是关于x的方程x2-2x-5=0的一个实数根,
是关于x的方程x2-2x-5=0的一个实数根,
解得x1,2=1± ,
,
所以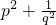 =2p2=2
=2p2=2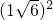 =14±4
=14±4 ;
;
故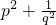 的值为14或14±4
的值为14或14±4 .
.
分析:本题可分两种情况进行分别求解.当p≠ 时,根据根与系数的关系求出所求的值;当p=
时,根据根与系数的关系求出所求的值;当p= 时,可直接求出方程的解,然后代入求解.
时,可直接求出方程的解,然后代入求解.
点评:本题主要考查根与系数的关系和一元二次方程的求解,应熟练掌握.
 时,p、
时,p、 是关于x的方程x2-2x-5=0的两个不相等的实数根,
是关于x的方程x2-2x-5=0的两个不相等的实数根,则p+
 =2,p•
=2,p• =-5,
=-5,所以
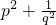 =
=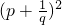 -2p•
-2p• =4-2×(-5)=14;
=4-2×(-5)=14;(2)当p=
 时,p、
时,p、 是关于x的方程x2-2x-5=0的一个实数根,
是关于x的方程x2-2x-5=0的一个实数根,解得x1,2=1±
 ,
,所以
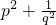 =2p2=2
=2p2=2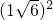 =14±4
=14±4 ;
;故
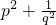 的值为14或14±4
的值为14或14±4 .
.分析:本题可分两种情况进行分别求解.当p≠
 时,根据根与系数的关系求出所求的值;当p=
时,根据根与系数的关系求出所求的值;当p= 时,可直接求出方程的解,然后代入求解.
时,可直接求出方程的解,然后代入求解.点评:本题主要考查根与系数的关系和一元二次方程的求解,应熟练掌握.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 的值.
的值. =4.
=4.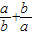 的值.
的值.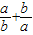 =
=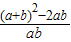 =4.
=4.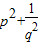 的值.
的值.