题目内容
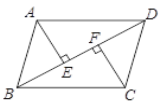
【题目】如图,在由6个大小相同的小正方形组成的方格中,设每个小正方形的边长均为1.
(1)如图①,![]() ,
,![]() ,
,![]() 是三个格点(即小正方形的顶点),判断
是三个格点(即小正方形的顶点),判断![]() 与
与![]() 的位置关系,并说明理由;
的位置关系,并说明理由;

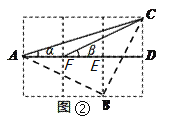
(2)如图②,连接三格和两格的对角线,求![]() 的度数(要求:画出示意图,并写出证明过程).
的度数(要求:画出示意图,并写出证明过程).

【答案】(1)![]() ,理由见解析;(2)
,理由见解析;(2)![]() ,理由见解析.
,理由见解析.
【解析】
(1)连接AC,再利用勾股定理列式求出AB2、BC2、AC2,然后利用勾股定理逆定理解答;
(2)根据勾股定理的逆定理判定△ABC是等腰直角三角形,根据全等三角形的判定和性质,可得结果.
解:(1)![]() ,
,
理由:如图①,连接![]() ,
,
由勾股定理可得![]() ,
,![]() ,
,![]() ,
,
所以![]() ,
,
所以![]() 是直角三角形且
是直角三角形且![]() ,
,
所以![]() ,
,

(2)![]() .
.
理由:如图②,连接AB 、BC,
由勾股定理得![]() ,
,
![]() ,
,
![]() ,
,
所以![]() ,
,
所以![]() 是直角三角形且
是直角三角形且![]() .
.
又因为![]() ,所以
,所以![]() 是等腰直角三角形,
是等腰直角三角形,
∴∠CAB=45°,
在△ABE和△FCD中,
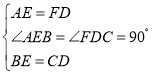 ,
,
∴△ABE≌△FCD(SAS),
∴∠BAD=∠β,
∴∠α+∠β=∠CAD+∠BAD=45°.

练习册系列答案
相关题目