��Ŀ����
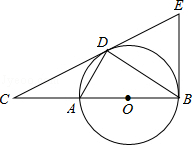
����Ŀ����֪����ͼ1����AOB�͡�COD������O��OB��OD�غϣ�OMΪ��AOD��ƽ���ߣ�ONΪ��BOC��ƽ���ߣ���AOB��������COD������
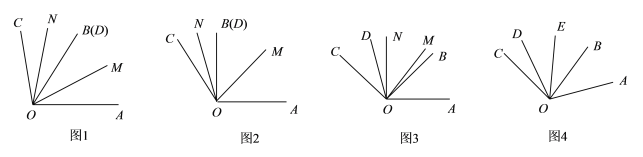
��1����ͼ2��������90�㣬����30�������MON��________��
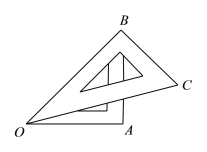
��2��������COD��O��ʱ����ת��ͼ3��λ�ã����MON��(����������ʾ)
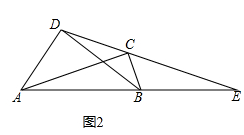
��3����ͼ4��������2������COD��O��ʱ����ת��ת��Ϊ3��/�룬��AOB��Oͬʱ��ʱ����ת��ת��Ϊ1��/��(ת��OC��OA����ʱֹͣ�˶�)����OEƽ�֡�BOD�����жϡ�COE���AOD��������ϵ��˵�����ɣ�
���𰸡���1��60�㣨2��![]() ����3��
����3��![]() Ϊ��ֵ
Ϊ��ֵ![]() ��
��
��������
��1�����ý�ƽ���ߵ����ʼ��ɵó���MON=![]() ��AOD+
��AOD+![]() ��BOC������������ɣ�
��BOC������������ɣ�
��2�����BOD=��������MOD=![]() =
=![]() ����NOB=
����NOB=![]() =
=![]() �������ó����ɣ�
�������ó����ɣ�
��3��������֪��ʾ����COE�͡�AOD�������ó��𰸣�
��1����OMΪ��AOD��ƽ���ߣ�ONΪ��BOC��ƽ���ߣ���AOB=������COD=�£���=90�b����=30�b��
���MON=![]() ��+
��+![]() ��=60�㣬
��=60�㣬
�ʴ�Ϊ��60�㣻
��2�����BOD������
�ߡ�MOD��![]() ��
��![]() ����NOB��
����NOB��![]() ��
��![]() ��
��
���MON����MOD����NOB����DOB��![]() ��
��![]() ������
������![]() ��
��
��3��![]() Ϊ��ֵ
Ϊ��ֵ![]() ��
��
���˶�ʱ��Ϊt�룬���DOB��3t��t��2t����DOE��![]() ��DOB��t��
��DOB��t��
���COE������t����AOD������2t��
�֡�����2����
���AOD��2����2t��2(����t)��
��![]() ��
��![]() ��
��

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�