题目内容
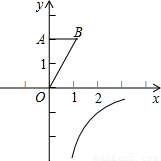
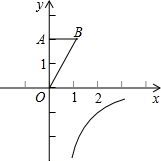 如图,OA在y轴上,点B在第一象限内,OA=2,OB=
如图,OA在y轴上,点B在第一象限内,OA=2,OB=| 5 |
| k |
| x |
-2
-2
.分析:利用勾股定理求出AB的长,作出图形,根据旋转变换只改变图形的位置不改变图形的形状与大小,可得OA′=OA,A′B′=AB,然后写出点B′的坐标,再利用待定系数法求反比例函数解析式解答.
解答: 解:在Rt△OAB中,∵OA=2,OB=
解:在Rt△OAB中,∵OA=2,OB=
,
∴AB=
=
=1,
∵△OA′B′是Rt△OAB绕点O顺时针方向旋转90°得到,
∴OA′=OA=2,A′B′=AB=1,
∴点B′(2,-1),
∵点B′在反比例函数y=
(x>0)的图象上,
∴
=-1,
解得k=-2.
故答案为:-2.
 解:在Rt△OAB中,∵OA=2,OB=
解:在Rt△OAB中,∵OA=2,OB=| 5 |
∴AB=
| OB2-OA2 |
|
∵△OA′B′是Rt△OAB绕点O顺时针方向旋转90°得到,
∴OA′=OA=2,A′B′=AB=1,
∴点B′(2,-1),
∵点B′在反比例函数y=
| k |
| x |
∴
| k |
| 2 |
解得k=-2.
故答案为:-2.
点评:本题考查了坐标与图形变化-旋转,待定系数法求反比例函数解析式,利用旋转变换只改变图形的位置不改变图形的形状与大小,求出旋转后的点B的对应点的坐标是解题的关键.

练习册系列答案
相关题目
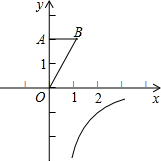 如图,OA在y轴上,点B在第一象限内,OA=2,OB=
如图,OA在y轴上,点B在第一象限内,OA=2,OB= ,若将△OAB绕点O按Rt△OAB的直角边顺时针方向旋转90°,此时点B恰好落在反比例函数y=
,若将△OAB绕点O按Rt△OAB的直角边顺时针方向旋转90°,此时点B恰好落在反比例函数y= (x>0)的图象上,则k的值是________.
(x>0)的图象上,则k的值是________.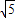 ,若将△OAB绕点O按Rt△OAB的直角边顺时针方向旋转90°,此时点B恰好落在反比例函数y=
,若将△OAB绕点O按Rt△OAB的直角边顺时针方向旋转90°,此时点B恰好落在反比例函数y=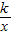 (x>0)的图象上,则k的值是 .
(x>0)的图象上,则k的值是 .
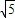 ,若将△OAB绕点O按Rt△OAB的直角边顺时针方向旋转90°,此时点B恰好落在反比例函数y=
,若将△OAB绕点O按Rt△OAB的直角边顺时针方向旋转90°,此时点B恰好落在反比例函数y= (x>0)的图象上,则k的值是 .
(x>0)的图象上,则k的值是 .