题目内容
如图是二次函数y=ax2+bx+c（a≠0）的图象，根据图象比较大小：a-b+c 0．
【答案】分析：分析题干：将x=-1代入方程得：y=a-b+c，再由函数的图象得，当x=-1时，y值在x轴上方，即y＞0，从而可得到a-b+c与0的大小关系．
解答：解：将x=-1代入函数得：y=a-b+c，由函数图象得：当x=-1时，y＞0，所以a-b+c＞0，故应填＞．
点评：解答此题应该结合二次函数的图象，根据二次函数图象可得当x=-1时，y＞0，从而可得a-b+c＞0．
解答：解：将x=-1代入函数得：y=a-b+c，由函数图象得：当x=-1时，y＞0，所以a-b+c＞0，故应填＞．
点评：解答此题应该结合二次函数的图象，根据二次函数图象可得当x=-1时，y＞0，从而可得a-b+c＞0．
练习册系列答案
阅读快车系列答案
相关题目
16、如图是二次函数y1=ax2+bx+c（a≠0）和一次函数y2=mx+n（m≠0）的图象，当y2＞y1，x的取值范围是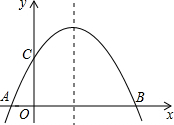
如图是二次函数y=2x2-4x-6的图象，那么方程2x2-4x-6=0的两根之和
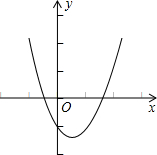如图是二次函数y=ax2+bx+c（a≠0）在平面直角坐标系中的图象，根据图形判断①c＞0；②a+b+c＜0；③2a-b＜0；④b2+8a＞4ac中正确的是（填写序号）
如图是二次函数
如图是二次函数y=ax2+bx+c的部分图象，由图象可知方程ax2+bx+c=0的解是