题目内容
如图,PA、PB是⊙O的两条切线,切点分别为A、B若直径AC=12cm,∠P=60°,求弦AB的长.
【答案】分析:连接CB.PA、PB是QO的切线,由切线长定理知PA=PB;又∠P=60°,则等腰三角形APB是等边三角形,则有ABP=60°;由弦切角定理知,∠PAB=∠C=60°,AC是直径;由直径对的圆周角是直角得∠ABC=90°,则在Rt△ABC中,有∠CAB=30°,进而可知AB=ACsin∠CAB=12× =6
=6 (若取近似值,不扣分).
(若取近似值,不扣分).
解答: 解:连接CB.
解:连接CB.
∵PA、PB是⊙O的切线,
∴PA=PB,
又∵∠P=60°,
∴∠PAB=60°;
又∵AC是⊙O的直径,
∴CA⊥PA,∠ABC=90°,
∴∠CAB=30°,
而AC=12,
∴在Rt△ABC中,cos30°= ,
,
∴AB=12× =6
=6 (若取近似值,不扣分).
(若取近似值,不扣分).
点评:本题利用了切线长定理,等边三角形的判定和性质,弦切角定理,直角三角形的性质,正弦的概念求解.注意本题的解法不唯一.
 =6
=6 (若取近似值,不扣分).
(若取近似值,不扣分).解答:
 解:连接CB.
解:连接CB.∵PA、PB是⊙O的切线,
∴PA=PB,
又∵∠P=60°,
∴∠PAB=60°;
又∵AC是⊙O的直径,
∴CA⊥PA,∠ABC=90°,
∴∠CAB=30°,
而AC=12,
∴在Rt△ABC中,cos30°=
 ,
,∴AB=12×
 =6
=6 (若取近似值,不扣分).
(若取近似值,不扣分).点评:本题利用了切线长定理,等边三角形的判定和性质,弦切角定理,直角三角形的性质,正弦的概念求解.注意本题的解法不唯一.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
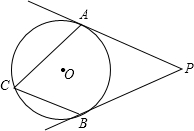 如图,PA,PB是⊙O的切线,切点分别为A,B,且∠APB=50°,点C是优弧
如图,PA,PB是⊙O的切线,切点分别为A,B,且∠APB=50°,点C是优弧
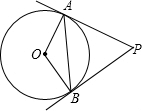 如图,PA、PB是⊙O的切线,A、B为切点,∠OAB=30度.
如图,PA、PB是⊙O的切线,A、B为切点,∠OAB=30度. 4、如图,PA、PB是⊙O的两条切线,A、B是切点,连接AB,直线PO交AB于M.请你根据圆的对称性,写出△PAB的三个正确的结论.
4、如图,PA、PB是⊙O的两条切线,A、B是切点,连接AB,直线PO交AB于M.请你根据圆的对称性,写出△PAB的三个正确的结论.
 (2012•谷城县模拟)如图,PA、PB是⊙O 的切线,切点分别是A、B,点C是⊙O上异与点A、B的点,如果∠P=60°,那么∠ACB等于
(2012•谷城县模拟)如图,PA、PB是⊙O 的切线,切点分别是A、B,点C是⊙O上异与点A、B的点,如果∠P=60°,那么∠ACB等于