题目内容
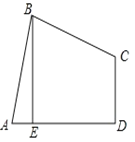
【题目】如图,正方形ABCD的边长为4,点E在对角线BD上,且∠BAE=22.5°,则BE的长为( )

A.![]() B.2C.4
B.2C.4![]() ﹣4D.4﹣2
﹣4D.4﹣2![]()
【答案】C
【解析】
连接AC,交BD与O,过E作EF⊥AB,由正方形的性质可求出OB的长,可得∠ABD=∠BAC=45°,即可证明AE为∠BAC的角平分线,△BEF是等腰直角三角形,根据角平分线的性质可得EF=OE=BF,根据BE=OB-OE,在等腰直角三角形BEF中,根据BE=![]() EF即可求出EF的长,进而求出BE的长即可.
EF即可求出EF的长,进而求出BE的长即可.
连接AC,交BD与O,过E作EF⊥AB,
∵ABCD是正方形,
∴BD⊥AC,∠ABD=∠BAC=45°,OB=![]() AB=2
AB=2![]() ,
,
∵∠BAE=22.5°,
∴AE为∠BAC的角平分线,
∵EF⊥AB,OB⊥OA,
∴EF=OE,
∵∠ABD=45°,
∴△BED是等腰直角三角形,
∴BE=![]() EF,
EF,
∴OB-EF=![]() EF,
EF,
解得EF=4-2![]() ,
,
∴BE=![]() (4-2
(4-2![]() )=4
)=4![]() -4,
-4,

故选C.

 综合自测系列答案
综合自测系列答案【题目】甲、乙、丙三位运动员在相同条件下各射靶10次,每次射靶的成绩如下:
甲:9,10,8,5,7,8,10,8,8,7;
乙:5,7,8,7,8,9,7,9,10,10;
丙:7,6,8,5,4,7,6,3,9,5.
(1)根据以上数据完成下表:
平均数 | 中位数 | 方差 | |
甲 | 8 | 8 | |
乙 | 8 | 8 | 2.2 |
丙 | 6 | 3 |
(2)依据表中数据分析,哪位运动员的成绩最稳定,并简要说明理由;
(3)比赛时三人依次出场,顺序由抽签方式决定.求甲、乙相邻出场的概率.
【题目】东莞市出租车收费标准如下表所示,根据此收费标准,解决下列问题:
行驶路程 | 收费标准 |
不超出 | 起步价8元 |
超出 | 2.6元/ |
(1)若行驶路程为![]() ,则打车费用为______元;
,则打车费用为______元;
(2)若行驶路程为![]() ,则打车费用为______元(用含
,则打车费用为______元(用含![]() 的代数式表示);
的代数式表示);
(3)某同学周末放学回家,已知打车费用为34元,则他家离学校多少千米?